-
The first component,
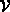 , is a finite, non-empty set.
The elements of
, is a finite, non-empty set.
The elements of 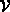 are called the vertices of G.
are called the vertices of G. -
The second component,
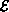 ,
is a finite set of ordered pairs of vertices.
I.e.,
,
is a finite set of ordered pairs of vertices.
I.e., 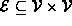 .
The elements of
.
The elements of 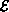 are called the edges of G.
are called the edges of G.
We begin with the definition of a directed graph:
Definition (Directed Graph) A directed graph , or digraph , is an ordered pairwith the following properties:
- The first component,
, is a finite, non-empty set. The elements of
are called the vertices of G.
- The second component,
, is a finite set of ordered pairs of vertices. I.e.,
. The elements of
are called the edges of G.
For example, consider the directed graph ![]() comprised of four vertices and six edges:
comprised of four vertices and six edges:
![]()
The graph G can be represented
graphically as shown in Figure ![]() .
The vertices are represented by appropriately labeled circles,
and the edges are represented by arrows
that connect associated vertices.
.
The vertices are represented by appropriately labeled circles,
and the edges are represented by arrows
that connect associated vertices.
Notice that because the pairs that represent edges are ordered,
the two edges (a,c) and (c,a) are distinct.
Furthermore, since ![]() is a mathematical set,
it cannot contain more than one instance of a given edge.
And finally, an edge such as (d,d) may connect a node to itself.
is a mathematical set,
it cannot contain more than one instance of a given edge.
And finally, an edge such as (d,d) may connect a node to itself.