Dijkstra's algorithm
is a greedy algorithm for solving
the single-source, shortest-path problem on an edge-weighted graph
in which all the weights are non-negative.
It finds the shortest paths from some initial vertex, say ![]() ,
to all the other vertices one-by-one.
The essential feature of Dijkstra's algorithm
is the order in which the paths are determined:
The paths are discovered in the order of their weighted lengths,
starting with the shortest, proceeding to the longest.
,
to all the other vertices one-by-one.
The essential feature of Dijkstra's algorithm
is the order in which the paths are determined:
The paths are discovered in the order of their weighted lengths,
starting with the shortest, proceeding to the longest.
For each vertex v,
Dijkstra's algorithm keeps track of three pieces of information,
![]() ,
, ![]() , and
, and ![]() :
:
Initially, ![]() for all
for all ![]() such that
such that ![]() ,
while
,
while ![]() .
.
Initially, ![]() is unknown for all
is unknown for all ![]() .
.
Dijkstra's algorithm proceeds in phases. The following steps are performed in each pass:
Table ![]() illustrates the operation of Dijkstra's
algorithm as it finds the shortest paths starting from vertex b
in graph
illustrates the operation of Dijkstra's
algorithm as it finds the shortest paths starting from vertex b
in graph ![]() shown in Figure
shown in Figure ![]() .
.
| passes | |||||||||||||||||||||||||||||||||||
|
vertex | initially | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||||||||||||||||||
| a | | 3 | b | | 3 | b | | 3 | b | | 3 | b | | 3 | b | | 3 | b | |||||||||||||||||
| b | 0 | -- | | 0 | -- | | 0 | -- | | 0 | -- | | 0 | -- | | 0 | -- | | 0 | -- | |||||||||||||||
| c | | 5 | b | 4 | a | | 4 | a | | 4 | a | | 4 | a | | 4 | a | ||||||||||||||||||
| d | | | | 6 | c | | 6 | c | | 6 | c | | 6 | c | |||||||||||||||||||||
| e | | | | 8 | c | 8 | c | | 8 | c | | 8 | c | ||||||||||||||||||||||
| f | | | | | 11 | d | 9 | e | | 9 | e | ||||||||||||||||||||||||
Initially all the tentative distances are ![]() ,
except for vertex b which has tentative distance zero.
Therefore, vertex b is selected in the first pass.
The mark
,
except for vertex b which has tentative distance zero.
Therefore, vertex b is selected in the first pass.
The mark ![]() beside an entry in Table
beside an entry in Table ![]() indicates that the shortest path is known (
indicates that the shortest path is known ( ![]() ).
).
Next we follow the edges emanating from vertex b,
![]() and
and ![]() ,
and update the distances accordingly.
The new tentative distances for a becomes 3
and the new tentative distance for c is 5.
In both cases, the next-to-last vertex on the shortest path is vertex b.
,
and update the distances accordingly.
The new tentative distances for a becomes 3
and the new tentative distance for c is 5.
In both cases, the next-to-last vertex on the shortest path is vertex b.
In the second pass, vertex a is selected and
its entry is marked with ![]() indicating the shortest path is known.
There is one edge emanating from a,
indicating the shortest path is known.
There is one edge emanating from a, ![]() .
The distance to c via a is 4.
Since this is less than the tentative distance to c,
vertex c is given the new tentative distance 4
and its predecessor on the shortest-path is set to a.
The algorithm continues in this fashion
for a total of
.
The distance to c via a is 4.
Since this is less than the tentative distance to c,
vertex c is given the new tentative distance 4
and its predecessor on the shortest-path is set to a.
The algorithm continues in this fashion
for a total of ![]() passes
until all the shortest paths have been found.
passes
until all the shortest paths have been found.
The shortest-path information contained in the right-most column
of Table ![]() can be represented in the form of a vertex-weighted graph
as shown in Figure
can be represented in the form of a vertex-weighted graph
as shown in Figure ![]() .
.
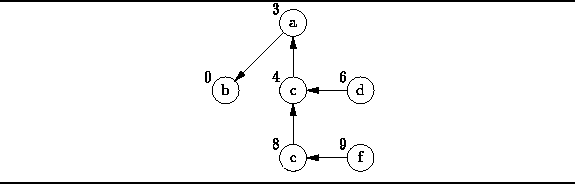
Figure: The Shortest-Path Graph for ![]()
This graph contains the same set of vertices as the problem graph ![]() .
Each vertex v is labeled with the length
.
Each vertex v is labeled with the length ![]() of the shortest path from b to v.
Each vertex (except b) has a single emanating edge
that connects the vertex to the next-to-last vertex on the shortest-path.
By following the edges in this graph from any vertex v to vertex b,
we can construct the shortest path from b to v in reverse.
of the shortest path from b to v.
Each vertex (except b) has a single emanating edge
that connects the vertex to the next-to-last vertex on the shortest-path.
By following the edges in this graph from any vertex v to vertex b,
we can construct the shortest path from b to v in reverse.