Floyd's Algorithm

Floyd's algorithm  uses the dynamic programming method to solve the all-pairs shortest-path problem on a dense graph. The method makes efficient use of an adjacency matrix to solve the problem. Consider an edge-weighted graph , where C(v,w) represents the weight on edge (v,w). Suppose the vertices are numbered from 1 to . I.e., let . Furthermore, let be the set comprised of the first k vertices in . I.e., , for .

Let be the shortest path from vertex v to w that passes only through vertices in , if such a path exists. I.e., the path has the form

Let be the length of path :

Since , the paths are correspond to the edges of G:

Therefore, the path lengths correspond to the weights on the edges of G:

Floyd's algorithm computes the sequence of matrices . The distances in represent paths with intermediate vertices in . Since , we can obtain the distances in from those in by considering only the paths that pass through vertex . Figure  illustrates how this is done.

  
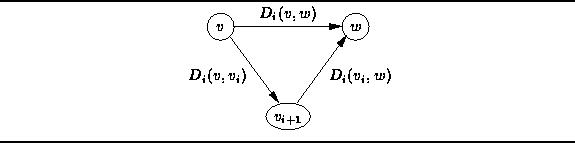
Figure: Calculating in Floyd's Algorithm

For every pair of vertices (v,w), we compare the distance , (which represents the shortest path from v to w that does not pass through ) with the sum (which represents the shortest path from v to w that does pass through ). Thus, is computed as follows:

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.