Consider the function f(n)=8n+128 shown in Figure ![]() .
Clearly, f(n) is non-negative for all integers
.
Clearly, f(n) is non-negative for all integers ![]() .
We wish to show that
.
We wish to show that ![]() .
According to Definition
.
According to Definition ![]() ,
in order to show this we need to find an integer
,
in order to show this we need to find an integer ![]() and a constant c>0
such that for all integers
and a constant c>0
such that for all integers ![]() ,
, ![]() .
.
It does not matter what the particular constants are--as long as they exist! E.g., suppose we choose c=1. Then
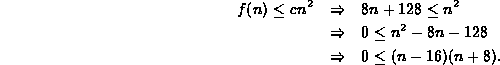
Since (n+8)>0 for all values of ![]() ,
we conclude that
,
we conclude that ![]() .
I.e.,
.
I.e., ![]() .
.
So, we have that for c=1 and ![]() ,
, ![]() for all integers
for all integers ![]() .
Hence,
.
Hence, ![]() .
Figure
.
Figure ![]() clearly shows
that the function
clearly shows
that the function ![]() is greater than
the function f(n)=8n+128 to the right of n=16.
is greater than
the function f(n)=8n+128 to the right of n=16.
Of course, there are many other values of c and ![]() that will do.
For example, c=2
and
that will do.
For example, c=2
and ![]() will do,
as will c=4 and
will do,
as will c=4 and ![]() .
(See Figure
.
(See Figure ![]() ).
).