Data Structures and Algorithms
with Object-Oriented Design Patterns in C++ 
In this section we examine some of the mathematical properties of big oh.
In particular, suppose we know that 
and 
.
and 
?
(Theorems 
and ). and ?
(Theorems and ). and 
related when
?
(Theorem ).
The first theorem addresses the asymptotic behavior of the sum of two functions whose asymptotic behaviors are known:
Theorem If
extbfProof
By Definition , there exist two integers, 
and 
and two constants 
and 
such that
for 
and
for 
.
Let 
and 
.
Consider the sum 
for 
:
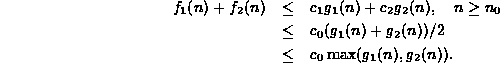
Thus, 
.
According to Theorem ,
if we know that functions and are
and 
, respectively,
the sum is 
.
The meaning of 
is this context is
the function h(n) where 
for integers all 
.
For example, consider the functions 
and
.
Then
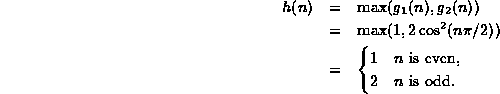
Theorem helps us simplify the asymptotic analysis
of the sum of functions by allowing us to drop the 
required by Theorem in certain circumstances:
Theorem Ifin which
for some limit
, then
.
extbfProof According to the definition of limits , the notation
means that, given any arbitrary positive value 
,
it is possible to find a value 
such that for all
Thus, if we chose a particular value, say 
,
then there exists a corresponding such that
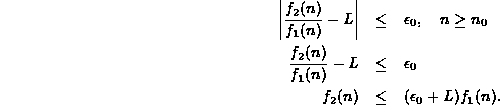
Consider the sum :
where 
.
Thus, .
Consider a pair of functions and ,
which are known to be and , respectively.
According to Theorem ,
the sum is .
However, Theorem says that,
if 
exists,
then the sum f(n) is simply 
which,
by the transitive property (see Theorem below), is .
In other words, if the ratio 
asymptotically approaches a constant as n gets large,
we can say that is ,
which is often a lot simpler than .
Theorem is particularly useful result.
Consider 
and 
.
From this we can conclude that 
.
Thus, Theorem suggests that
the sum of a series of powers of n is 
,
where m is the largest power of n in the summation.
We will confirm this result in Section below.
The next theorem addresses the asymptotic behavior of the product of two functions whose asymptotic behaviors are known:
Theorem If
extbfProof
By Definition , there exist two integers, and
and two constants and such that
for and
for .
Furthermore, by Definition ,
and are both non-negative for all integers .
Let and 
.
Consider the product 
for :
Thus, 
.
Theorem describes a simple,
but extremely useful property of big oh.
Consider the functions 
and
.
By Theorem ,
the asymptotic behavior of the product
is 
.
I.e., we are able to determine the asymptotic behavior of
the product without having to go through the gory details of
calculating that 
.
The next theorem is closely related to the preceding one in that it also shows how big oh behaves with respect to multiplication.
Theorem If
extbfProof
By Definition , there exist integers
and constant 
such that
for .
Since is never negative,
Thus, 
.
Theorem applies when we multiply a function, ,
whose asymptotic behavior is known to be ,
by another function .
The asymptotic behavior of the result is simply 
.
One way to interpret Theorem
is that it allows us to do the following mathematical manipulation:
I.e., Fallacy notwithstanding,
we can multiply both sides of the ``equation'' by
and the ``equality'' still holds.
Furthermore, when we multiply by ,
we simply bring the inside the 
.
The last theorem in this section introduces the transitive property of big oh:
Theorem (Transitive Property) If f(n)=O(g(n)) and g(n)=O(h(n)) then f(n)=O(h(n)).
extbfProof
By Definition , there exist two integers, and
and two constants and such that
for and
for .
Let and . Then
Thus, f(n)=O(h(n)).
The transitive property of big oh
is useful in conjunction with Theorem .
Consider 
which is clearly 
.
If we add to the function 
,
then by Theorem ,
the sum is
because 
.
I.e., 
.
The combination of the fact that 
and the transitive property of big oh,
allows us to conclude that the sum is .
Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.
