Data Structures and Algorithms with Object-Oriented Design Patterns in C#
next up previous contents index

Binomial Trees

A binomial tree is a general tree with a very special shape:

Definition (Binomial Tree)  The binomial tree of order tex2html_wrap_inline60665 with root R is the tree tex2html_wrap_inline65731 defined as follows
  1. If k=0, tex2html_wrap_inline65735. That is, the binomial tree of order zero consists of a single node, R.
  2. If k>0, tex2html_wrap_inline65741. That is, the binomial tree of order k>0 comprises the root R, and k binomial subtrees, tex2html_wrap_inline65749, tex2html_wrap_inline65751, ..., tex2html_wrap_inline65753.

Figure gif shows the first five binomial trees, tex2html_wrap_inline65749- tex2html_wrap_inline65757. It follows directly from Definition gif that the root of tex2html_wrap_inline65731, the binomial tree of order k, has degree k. Since k may arbitrarily large, so too can the degree of the root. Furthermore, the root of a binomial tree has the largest fanout of any of the nodes in that tree.

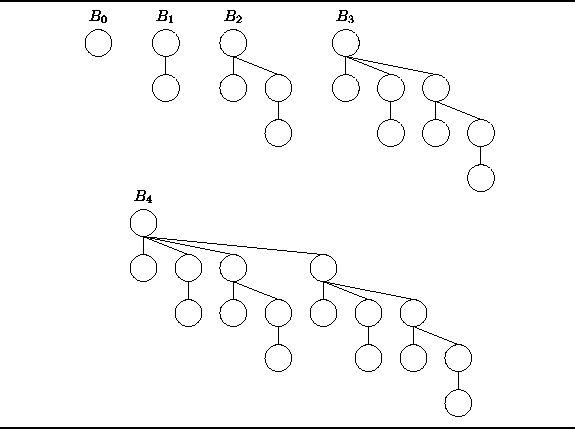
   figure25974
Figure: Binomial trees tex2html_wrap_inline65749, tex2html_wrap_inline65751, ..., tex2html_wrap_inline65757.

The number of nodes in a binomial tree of order k is a function of k:

Theorem  The binomial tree of order k, tex2html_wrap_inline65731, contains tex2html_wrap_inline58045 nodes.

extbfProof (By induction). Let tex2html_wrap_inline65793 be the number of nodes in tex2html_wrap_inline65731, a binomial tree of order k.

Base Case By definition, tex2html_wrap_inline65749 consists a single node. Therefore tex2html_wrap_inline65801.

Inductive Hypothesis Assume that tex2html_wrap_inline65803 for tex2html_wrap_inline65805, for some tex2html_wrap_inline65807. Consider the binomial tree of order l+1:

displaymath65719

Therefore the number of nodes in tex2html_wrap_inline65811 is given by

eqnarray26254

Therefore, by induction on l, tex2html_wrap_inline65803 for all tex2html_wrap_inline60665.

It follows from Theorem gif that binomial trees only come in sizes that are a power of two. That is, tex2html_wrap_inline65819. Furthermore, for a given power of two, there is exactly one shape of binomial tree.

Theorem  The height of tex2html_wrap_inline65731, the binomial tree of order k, is k.

extbfProof (By induction). Let tex2html_wrap_inline65827 be the height of tex2html_wrap_inline65731, a binomial tree of order k.

Base Case By definition, tex2html_wrap_inline65749 consists a single node. Therefore tex2html_wrap_inline65835.

Inductive Hypothesis Assume that tex2html_wrap_inline65837 for tex2html_wrap_inline65805, for some tex2html_wrap_inline65807. Consider the binomial tree of order l+1:

displaymath65719

Therefore the height tex2html_wrap_inline65811 is given by

eqnarray26276

Therefore, by induction on l, tex2html_wrap_inline65837 for all tex2html_wrap_inline60665.

Theorem gif tells us that the height of a binomial tree of order k is k and Theorem gif tells us that the number of nodes is tex2html_wrap_inline65803. Therefore, the height of tex2html_wrap_inline65731 is exactly tex2html_wrap_inline59121.

Figure gif shows that there are two ways to think about the construction of binomial trees. The first way follows directly from the Definition gif. That is, binomial tex2html_wrap_inline65731 consists of a root node to which the k binomial trees tex2html_wrap_inline65749, tex2html_wrap_inline65751, ..., tex2html_wrap_inline65753 are attached as shown in Figure gif (a).

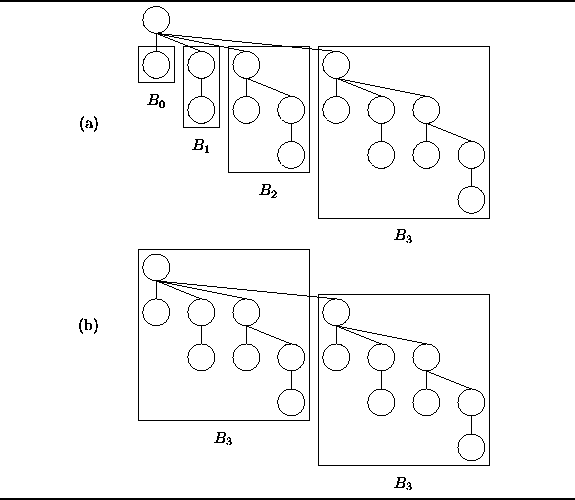
   figure26287
Figure: Two views of binomial tree tex2html_wrap_inline65757.

Alternatively, we can think of tex2html_wrap_inline65731 as being comprised of two binomial trees of order k-1. For example, Figure gif (b) shows that tex2html_wrap_inline65757 is made up of two instances of tex2html_wrap_inline65893. In general, suppose we have two trees of order k-1, say tex2html_wrap_inline65897 and tex2html_wrap_inline65899, where tex2html_wrap_inline65901. Then we can construct a binomial tree of order k by combining the trees to get

displaymath65721

Why do we call tex2html_wrap_inline65731 a binomial tree? It is because the number of nodes at a given depth in the tree is determined by the binomial coefficient. And the binomial coefficient derives its name from the binomial theorem. And the binomial theorem tells us how to compute the tex2html_wrap_inline57687 power of a binomial . And a binomial is an expression which consists of two terms, such as x+y. That is why it is called a binomial tree!

Theorem (Binomial Theorem)  The tex2html_wrap_inline57687 power of the binomial x+y for tex2html_wrap_inline58277 is given by

displaymath65722

where tex2html_wrap_inline65917 is called the binomial coefficient  .

extbfProof The proof of the binomial theorem is left as an exercise for the reader (Exercise gif).gif

The following theorem gives the expression for the number of nodes at a given depth in a binomial tree:

Theorem  The number of nodes at level l in tex2html_wrap_inline65731, the binomial tree of order k, where tex2html_wrap_inline65925, is given by the binomial coefficient tex2html_wrap_inline65927.

extbfProof (By induction). Let tex2html_wrap_inline65929 be the number of nodes at level l in tex2html_wrap_inline65731, a binomial tree of order k.

Base Case Since tex2html_wrap_inline65749 contains a single node, there is only one level in the tree, l=0, and exactly one node at that level. Therefore, tex2html_wrap_inline65941.

Inductive Hypothesis Assume that tex2html_wrap_inline65943 for tex2html_wrap_inline65945, for some tex2html_wrap_inline62845. The binomial tree of order h+1 is composed of two binomial trees of height h, one attached under the root of the other. Hence, the number of nodes at level l in tex2html_wrap_inline65955 is equal to the number of nodes at level l in tex2html_wrap_inline65959 plus the number of nodes at level l-1 in tex2html_wrap_inline65959:

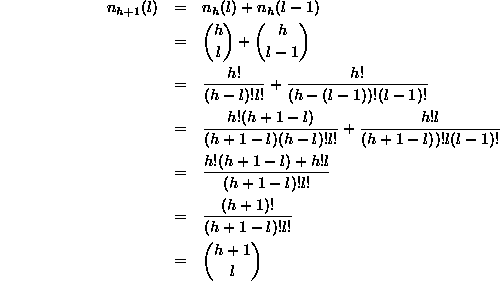
eqnarray26517

Therefore by induction on h, tex2html_wrap_inline65943.

next up previous contents index

Bruno Copyright © 2001 by Bruno R. Preiss, P.Eng. All rights reserved.