Topological Sort

Data Structures and Algorithms with Object-Oriented Design Patterns in C#

Topological Sort

A topological sort is an ordering of the vertices of a directed acyclic graph given by the following definition:

Definition (Topological Sort) Consider a directed acyclic graph . A topological sort of the vertices of G is a sequence in which each element of appears exactly once. For every pair of distinct vertices and in the sequence S, if is an edge in G, i.e., , then i<j.

Informally, a topological sort is a list of the vertices of a DAG in which all the successors of any given vertex appear in the sequence after that vertex. Consider the directed acyclic graph shown in Figure . The sequence is a topological sort of the vertices of . To see that this is so, consider the set of vertices:

The vertices in each edge are in alphabetical order, and so is the sequence S.

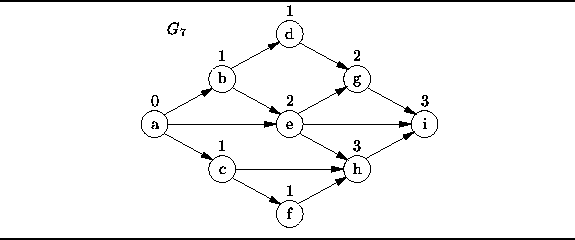
Figure: A directed acyclic graph.

It should also be evident from Figure that a topological sort is not unique. For example, the following are also valid topological sorts of the graph :

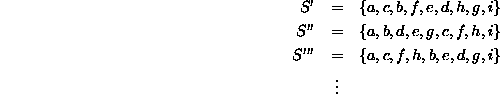
eqnarray50335

One way to find a topological sort is to consider the in-degrees of the vertices. (The number above a vertex in Figure is the in-degree of that vertex). Clearly the first vertex in a topological sort must have in-degree zero and every DAG must contain at least one vertex with in-degree zero. A simple algorithm to create the sort goes like this:

Repeat the following steps until the graph is empty:

Select a vertex that has in-degree zero.
Add the vertex to the sort.
Delete the vertex and all the edges emanating from it from the graph.