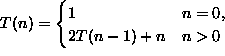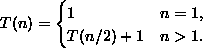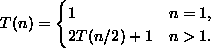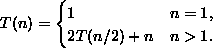Data Structures and Algorithms with Object-Oriented Design Patterns in C#

Exercises

1.   Determine the running times predicted by the detailed model of the computer given in Section  for each of the following program fragments:

   1. for (int i = 0; i < n; ++i)
          ++k;

   2. for (int i = 1; i < n; i *= 2)
          ++k;

   3. for (int i = n - 1; i != 0; i /= 2)
          ++k;

   4. for (int i = 0; i < n; ++i)
          if (i % 2 == 0)
              ++k;

   5. for (int i = 0; i < n; ++i)
          for (int j = 0; j < n; ++j)
              ++k;

   6. for (int i = 0; i < n; ++i)
          for (int j = i; j < n; ++j)
              ++k;

   7. for (int i = 0; i < n; ++i)
          for (int j = 0; j < i * i; ++j)
              ++k;

2. Repeat Exercise , this time using the simplified model of the computer given in Section .
3. Prove by induction the following summation formulas:
   1. 
   2. 
   3. 
4. Evaluate each of the following series summations:
   1. 
   2. 
   3. 
   4. 
5. Show that , for . Hint: Let and show that .
6. Show that . Hint: Let and show that the difference is (approximately) a geometric series summation.
7. Solve each of the following recurrences by repeated substitution:
   1. 
   2. 
   3. 
   4. 
   5. 
   6. 
   7. 

Copyright © 2001 by Bruno R. Preiss, P.Eng. All rights reserved.