|
Data Structures and Algorithms
with Object-Oriented Design Patterns in C# |
In this section we reexamine the asymptotic behavior of polynomials in n.
In Section 
we showed that 
.
That is, f(n) grows asymptotically no more quickly than 
.
This time we are interested in the asymptotic lower bound
rather than the asymptotic upper bound.
We will see that as n gets large,
the term involving also dominates the lower bound
in the sense that f(n) grows asymptotically as quickly as .
That is, that 
.
Theorem Consider a polynomial in n of the form
where
. Then
extbfProof
We begin by taking the term 
out of the summation:
Since, n is a non-negative integer and ,
the term is positive.
For each of the remaining terms in the summation, 
.
Hence
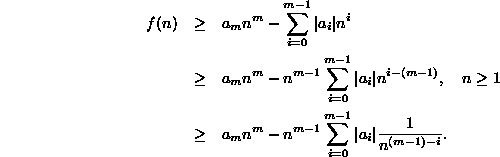
Note that for integers 
,
for 
.
Thus
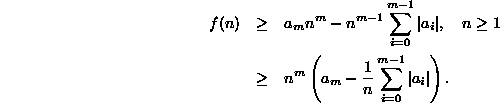
Consider the term in parentheses on the right.
What we need to do is to find a positive constant c
and an integer 
so that for all integers 
this term is greater than or equal to c:
We choose the value for which the term is greater than zero:
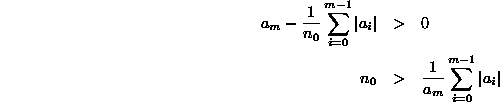
The value
will suffice!
Thus
From Equation we see that
we have found the constants and c,
such that for all , 
.
Thus, .
This property of the asymptotic behavior of polynomials
is used extensively.
In fact, whenever we have a function,
which is a polynomial in n,
we will immediately ``drop'' the less significant terms
(i.e., terms involving powers of n which are less than m),
as well as the leading coefficient, 
,
to write .
Copyright © 2001 by Bruno R. Preiss, P.Eng. All rights reserved.
