Searching a Binary Tree

Data Structures and Algorithms with Object-Oriented Design Patterns in Java

Searching a Binary Tree

The search method described above applies directly to binary search trees. As above, the search begins at the root node of the tree. If the object of the search, x, matches the root r, the search terminates successfully. If it does not, then if x is less than r, the left subtree is searched; otherwise x must be greater than r, in which case the right subtree is searched.

Figure shows two binary search trees. The tree is an example of a particularly bad search tree because it is not really very tree-like at all. In fact, it is topologically isomorphic with a linear, linked list. In the worst case, a tree which contains n items has height O(n). Therefore, in the worst case an unsuccessful search must visit O(n) internal nodes.

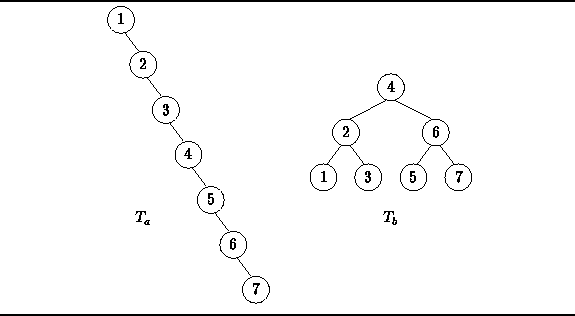
Figure: Examples of search trees.

On the other hand, tree in Figure is an example of a particularly good binary search tree. This tree is an instance of a perfect binary tree .

Definition (Perfect Binary Tree) A perfect binary tree of height is a binary tree with the following properties:
If h=0, then and .
Otherwise, h>0, in which case both and are both perfect binary trees of height h-1.

It is fairly easy to show that a perfect binary tree of height h has exactly internal nodes. Conversely, the height of a perfect binary tree with n internal nodes is . If we have a search tree that has the shape of a perfect binary tree, then every unsuccessful search visits exactly h+1 internal nodes, where . Thus, the worst case for unsuccessful search in a perfect tree is .