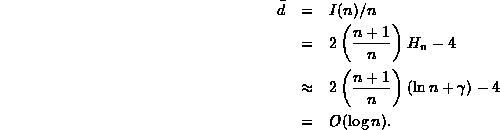Solving The Recurrence-Telescoping

This section presents a technique for solving recurrence relations such as Equation  called telescoping . The basic idea is this: We rewrite the recurrence formula so that a similar functional form appears on both sides of the equal sign. For example, in this case, we consider n>2 and divide both sides of Equation  by n+1 to get

Since this equation is valid for any n>2, we can write the following series of equations:

Each subsequent equation in this series is obtained by substituting n-1 for n in the preceding equation. In principle, we repeat this substitution until we get an expression on the right-hand-side involving the base case. In this example, we stop at n-k-1=2.

Because Equation  has a similar functional form on both sides of the equal sign, when we add Equation  through Equation  together, most of the terms cancel leaving

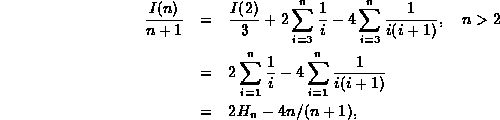
where is the harmonic number . In Section  it is shown that , where is called Euler's constant . Thus, we get that the average internal path length of the average binary search tree with n internal nodes is

Finally, we get to the point: The average depth of a node in the average binary search tree with n nodes is

Copyright © 1998 by Bruno R. Preiss, P.Eng. All rights reserved.