Example-Matrix Multiplication

Consider the problem of computing the product of two matrices. That is, given two matrices, A and B, compute the matrix , the elements of which are given by

Section  shows that the direct implementation of Equation  results in an running time. In this section we show that the use of a divide-and-conquer strategy results in a slightly better asymptotic running time.

To implement a divide-and-conquer algorithm we must break the given problem into several subproblems that are similar to the original one. In this instance we view each of the matrices as a matrix, the elements of which are submatrices. Thus, the original matrix multiplication, can be written as

where each , , and is an matrix.

From Equation  we get that the result submatrices can be computed as follows:

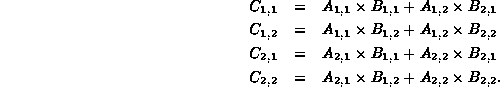
Here the symbols + and are taken to mean addition and multiplication (respectively) of matrices.

In order to compute the original matrix multiplication we must compute eight matrix products (divide) followed by four matrix sums (conquer). Since matrix addition is an operation, the total running time for the multiplication operation is given by the recurrence:

Note that Equation  is an instance of the general recurrence given in Equation . In this case, a=8, b=2, and k=2. We can obtain the solution directly from Equation . Since , the total running time is . But this no better than the original, direct algorithm!

Fortunately, it turns out that one of the eight matrix multiplications is redundant. Consider the following series of seven matrices:

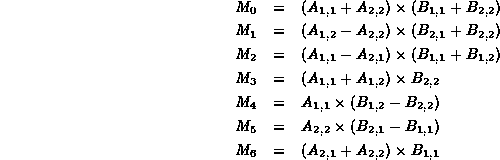
Each equation above has only one multiplication. Ten additions and seven multiplications are required to compute through . Given through , we can compute the elements of the product matrix C as follows:

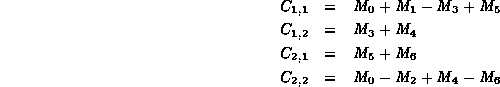
Altogether this approach requires seven matrix multiplications and 18 additions. Therefore, the worst-case running time is given by the following recurrence:

As above, Equation  is an instance of the general recurrence given in Equation . and we obtain the solution directly from Equation . In this case, a=7, b=2, and k=2. Therefore, and the total running time is

Note . Consequently, the running time of the divide-and-conquer matrix multiplication strategy is which is better (asymptotically) than the straightforward approach.

Copyright © 1998 by Bruno R. Preiss, P.Eng. All rights reserved.