 is an
integer power of two. Relaxing these assumptions does not change the
essential character of the algorithm but would complicate the
presentation.
is an
integer power of two. Relaxing these assumptions does not change the
essential character of the algorithm but would complicate the
presentation.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
Sorting is a common and important problem in computing. Given a
sequence of N
data elements, we are required to generate an
ordered sequence that contains the same elements. Here, we present a
parallel version of the well-known mergesort algorithm. The
algorithm assumes that the sequence to be sorted is distributed and so
generates a distributed sorted sequence. For simplicity, we assume
that N
is an integer multiple of P
, that the N
data
are distributed evenly among P
tasks, and that  is an
integer power of two. Relaxing these assumptions does not change the
essential character of the algorithm but would complicate the
presentation.
is an
integer power of two. Relaxing these assumptions does not change the
essential character of the algorithm but would complicate the
presentation.
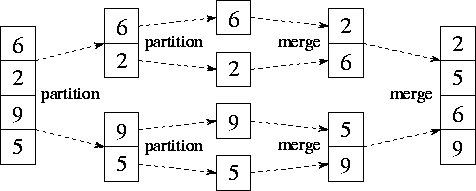
Figure 11.4: Mergesort, used here to sort the sequence [6,2,9,5].
The two partition phases each split the input sequence; the two merge
phases each combine two sorted subsequences generated in a previous
phase.
The sequential mergesort algorithm is as follows; its execution is illustrated in Figure 11.4.
The merge operation employed in step (4) combines two sorted
subsequences to produce a single sorted sequence. It repeatedly
compares the heads of the two subsequences and outputs the lesser
value until no elements remain. Mergesort requires 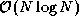 time to sort N
elements, which is the best that can be achieved
(modulo constant factors) unless data are known to have special
properties such as a known distribution or degeneracy.
time to sort N
elements, which is the best that can be achieved
(modulo constant factors) unless data are known to have special
properties such as a known distribution or degeneracy.
We first describe two algorithms required in the implementation of parallel mergesort: compare-exchange and parallel merge.
A compare-exchange operation merges two sorted sequences of length M , contained in tasks A and B . Upon completion of the operation, both tasks have M data, and all elements in task A are less than or equal to all elements in task B . As illustrated in Figure 11.5, each task sends its data to the other task. Task A identifies the M lowest elements and discards the remainder; this process requires at least M/2 and at most M comparisons. Similarly, task B identifies the M highest elements.
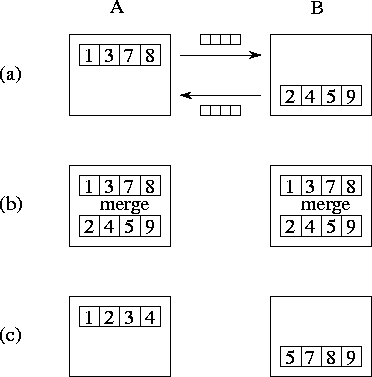
Figure 11.5: The compare-exchange algorithm, with M=4
. (a) Tasks
A
and B
exchange their sorted subsequences. (b) They perform a
merge operation to identify the lowest and highest M
elements,
respectively. (c) Other elements are discarded, leaving a single
sorted sequence partitioned over the two tasks.
Notice that a task may not need all M of its neighbor's data in order to identify the M lowest (or highest) values. On average, only M/2 values are required. Hence, it may be more efficient in some situations to require the consumer to request data explicitly. This approach results in more messages that contain a total of less than M data, and can at most halve the amount of data transferred.
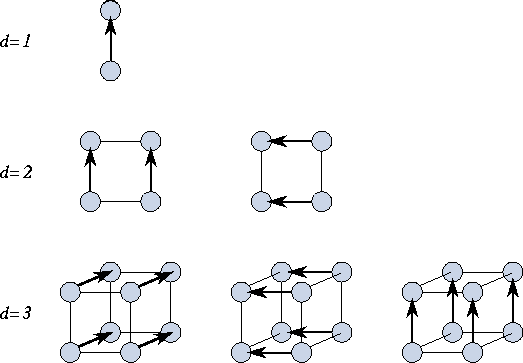
Figure 11.6: The parallel merge operation, performed in hypercubes
of dimension one, two, and three. In a hypercube of dimension
d
, each task performs d
compare-exchange operations. Arrows
point from the ``high'' to the ``low'' task in each
exchange.
A parallel merge algorithm performs a merge operation on two sorted
sequences of length  , each distributed over
, each distributed over 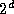 tasks, to
produce a single sorted sequence of length
tasks, to
produce a single sorted sequence of length 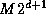 distributed over
distributed over
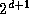 tasks. As illustrated in Figure 11.6, this is
achieved by using the hypercube communication template. Each of the
tasks. As illustrated in Figure 11.6, this is
achieved by using the hypercube communication template. Each of the
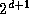 tasks engages in d+1
compare-exchange steps, one with
each neighbor. In effect, each node executes
Algorithm 11.1, applying the following operator at each
step.
tasks engages in d+1
compare-exchange steps, one with
each neighbor. In effect, each node executes
Algorithm 11.1, applying the following operator at each
step.
if ( myid AND> 0 ) then
state = compare_exchange_high(state,message)
else
state = compare_exchange_low(state,message)
endif
In this code fragment, AND is a bitwise logical and operator, used to determine whether the task is ``high'' or ``low'' in a particular exchange; myid and i are as in Algorithm 11.1.
We next describe the parallel mergesort algorithm proper. Each task in the computation executes the following logic.
procedure parallel_mergesort(myid, d, data, newdata)
begin
data = sequential_mergesort(data)
for dim = 1 to d
data = parallel_merge(myid, dim, data)
endfor
newdata = data
end
First, each task sorts its local sequence using sequential mergesort.
Second, and again using the hypercube communication structure, each of
the 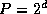 tasks executes the parallel merge algorithm d
times,
for subcubes of dimension 1.. d
. The i
th parallel merge
takes two sequences, each distributed over
tasks executes the parallel merge algorithm d
times,
for subcubes of dimension 1.. d
. The i
th parallel merge
takes two sequences, each distributed over 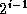 tasks, and
generates a sorted sequence distributed over
tasks, and
generates a sorted sequence distributed over 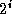 tasks. After
d
such merges, we have a single sorted list distributed over
tasks. After
d
such merges, we have a single sorted list distributed over
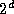 tasks.
tasks.
Parallel mergesort uses the hypercube communication template at
multiple levels. We review these uses and develop a performance
model. We assume N
data distributed over 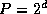 tasks (that
is,
tasks (that
is, 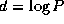 ), with N
an integer multiple of P
. Hence,
the total number of compare-exchanges is
), with N
an integer multiple of P
. Hence,
the total number of compare-exchanges is

Because each compare-exchange requires one message containing N/P data, the per-processor communication cost is
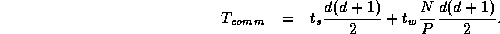
The computation costs comprise the initial intraprocessor sort and the
comparisons performed during the interprocessor communication phase.
The former involves a total of 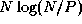 comparisons, while the
latter requires at most
comparisons, while the
latter requires at most 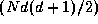 comparisons, thereby giving
computation costs summed over P
processors of
comparisons, thereby giving
computation costs summed over P
processors of
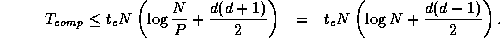
Because the algorithm is perfectly balanced, we can assume that idle time is negligible. Thus, we obtain the following model for parallel execution time:
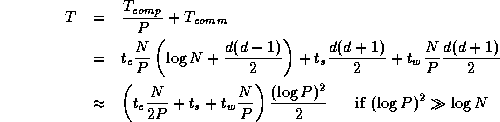
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
© Copyright 1995 by Ian Foster