


Type declarations and pattern matching
Although Objective CAML's predefined types permit the construction of data
structures from tuples and lists, one needs to be able to define new
types to describe certain data structures. In Objective CAML, type declarations
are recursive and may be parameterized by type variables, in the same vein
as the type 'a list already encountered. Type inference takes
these new declarations into account to produce the type of an expression.
The construction of values of these new types uses the constructors
described in their definition. A special feature of languages in the ML
family is pattern matching. It allows simple access to the
components of complex data structures. A function definition most often
corresponds to pattern matching over one of its parameters, allowing the
function to be defined by cases.
First of all we present pattern matching over the predefined types, and
then go on to describe the various ways to declare structured types and how
to construct values of such types, as well as how to access their
components through pattern matching.
Pattern matching
A pattern is not strictly speaking an Objective CAML expression. It's more like
a correct (syntactically, and from the point of view of types) arrangement
of elements such as constants of the primitive types (int,
bool, char, ..), variables, constructors, and the symbol
_ called the wildcard pattern. Other symbols are used in
writing patterns. We will introduce them to the extent needed.
Pattern matching applies to values. It is used to recognize the form of
this value and lets the computation be guided accordingly,
associating with each pattern an expression to compute.
Syntax
| match expr with |
| | p1 -> expr1 |
| : |
| | pn -> exprn |
The expression expr is matched sequentially to the various patterns
p1, ..., pn. If one of the patterns (for example
pi) is consistent with the value of expr then the
corresponding computation branch (expri) is evaluated. The
various patterns pi are of the same type. The same goes for
the various expressions expri. The vertical bar preceding the
first pattern is optional.
Examples
Here are two ways to define by pattern matching a function imply
of type (bool * bool) -> bool implementing logical
implication. A pattern which matches pairs has the form ( , ).
The first version of imply enumerates all possible cases, as a
truth table would:
# let imply v = match v with
(true,true) -> true
| (true,false) -> false
| (false,true) -> true
| (false,false) -> true;;
val imply : bool * bool -> bool = <fun>
By using variables which group together several cases, we obtain a more
compact definition.
# let imply v = match v with
(true,x) -> x
| (false,x) -> true;;
val imply : bool * bool -> bool = <fun>
These two versions of imply compute the same function. That is,
they return the same values for the same inputs.
Linear pattern
A pattern must necessarily be linear, that is, no given variable can
occur more than once inside the pattern being matched. Thus, we might have
hoped to be able to write:
# let equal c = match c with
(x,x) -> true
| (x,y) -> false;;
Characters 35-36:
This variable is bound several times in this matching
But this would have required the compiler to know how to carry out equality
tests. Yet this immediately raises numerous problems.
If we accept physical equality between values, we get a system which is too
weak, incapable of recognizing the equality between two occurrences of the
list [1; 2], for example. If we decide to use structural
equality, we run the risk of having to traverse, ad infinitum, circular
structures. Recursive functions, for example, are circular structures, but
we can construct recursive, hence circular, values which are not functions
as well (see page ??).
Wildcard pattern
The symbol _ matches all possible values. It is called a wildcard
pattern. It can be used to match complex types. We use it, for example,
to further simplify the definition of the function imply:
# let imply v = match v with
(true,false) -> false
| _ -> true;;
val imply : bool * bool -> bool = <fun>
A definition by pattern matching must handle the entire set of possible
cases of the values being matched. If this is not the case, the compiler
prints a warning message:
# let is_zero n = match n with 0 -> true ;;
Characters 17-40:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
1
val is_zero : int -> bool = <fun>
Indeed if the actual parameter is different from 0 the function
doesn't know what value to return. So the case analysis can be completed
using the wildcard pattern.
# let is_zero n = match n with
0 -> true
| _ -> false ;;
val is_zero : int -> bool = <fun>
If, at run-time, no pattern is selected, then an exception is raised.
Thus, one can write:
# let f x = match x with 1 -> 3 ;;
Characters 11-30:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
0
val f : int -> int = <fun>
# f 1 ;;
- : int = 3
# f 4 ;;
Uncaught exception: Match_failure("", 11, 30)
The Match_Failure exception is raised by the call to f
4, and if it is not handled induces the computation in progress to halt
(see ??)
Combining patterns
Combining several patterns lets us obtain a new pattern which can
match a value according to one or another of the original patterns.
The syntactic form is as follows:
Syntax
p1 | ...| pn
It constructs a new pattern by combining the patterns p1, ...and pn. The only strong constraint is that all naming is
forbidden within these patterns. So each one of them must contain only
constant values or the wildcard pattern. The following example
demonstrates how to verify that a character is a vowel.
# let is_a_vowel c = match c with
'a' | 'e' | 'i' | 'o' | 'u' | 'y' -> true
| _ -> false ;;
val is_a_vowel : char -> bool = <fun>
# is_a_vowel 'i' ;;
- : bool = true
# is_a_vowel 'j' ;;
- : bool = false
Pattern matching of a parameter
Pattern matching is used in an essential way for defining functions by
cases. To make writing these definitions easier, the syntactic construct
function allows pattern matching of a parameter:
Syntax
| function |
| |
p1 -> expr1 |
| |
| |
p2 -> expr2 |
| |
|
: |
| |
| |
pn -> exprn |
The vertical bar preceding the first pattern is optional here as well. In
fact, like Mr. Jourdain, each time we define a function, we use
pattern matching7. Indeed, the
construction function x -> expression, is a
definition by pattern matching using a single pattern reduced to one
variable. One can make use of this detail with simple patterns as in:
# let f = function (x,y) -> 2*x + 3*y + 4 ;;
val f : int * int -> int = <fun>
In fact the form
function p1 -> expr1
| ...| pn -> exprn
is equivalent to
function expr -> match expr with
p1 -> expr1 | ...| pn -> exprn
Using the equivalence of the declarations mentioned on page
??, we write:
# let f (x,y) = 2*x + 3*y + 4 ;;
val f : int * int -> int = <fun>
But this natural way of writing is only possible if the value being matched
belongs to a type having only a single constructor. If such is not the
case, the pattern matching is not exhaustive:
# let is_zero 0 = true ;;
Characters 13-21:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
1
val is_zero : int -> bool = <fun>
Naming a value being matched
During pattern matching, it is sometimes useful to name part or all of the
pattern. The following syntactic form introduces the keyword as
which binds a name to a pattern.
Syntax
( p as name )
This is useful when one needs to take apart a value while still maintaining
its integrity. In the following example, the function min_rat
gives the smaller rational of a pair of rationals. The latter are each
represented by a numerator and denominator in a pair.
# let min_rat pr = match pr with
((_,0),p2) -> p2
| (p1,(_,0)) -> p1
| (((n1,d1) as r1), ((n2,d2) as r2)) ->
if (n1 * d2 ) < (n2 * d1) then r1 else r2;;
val min_rat : (int * int) * (int * int) -> int * int = <fun>
To compare two rationals, it is necessary to take them apart in order to
name their numerators and denominators (n1, n2,
d1 and d2), but the initial pair (r1 or
r2) must be returned. The as construct allows us to name the
parts of a single value in this way. This lets us avoid having to
reconstruct the rational returned as the result.
Pattern matching with guards
Pattern matching with guards corresponds to the evaluation of a conditional
expression immediately after the pattern is matched. If this expression
comes back true, then the expression associated with that pattern
is evaluated, otherwise pattern matching continues with the following
pattern.
Syntax
| match expr with |
| : |
| | pi when condi -> expri |
| : |
The following example uses two guards to test equality of two rationals.
# let eq_rat cr = match cr with
((_,0),(_,0)) -> true
| ((_,0),_) -> false
| (_,(_,0)) -> false
| ((n1,1), (n2,1)) when n1 = n2 -> true
| ((n1,d1), (n2,d2)) when ((n1 * d2) = (n2 * d1)) -> true
| _ -> false;;
val eq_rat : (int * int) * (int * int) -> bool = <fun>
If the guard fails when the fourth pattern is matched, matching continues with
the fifth pattern.
Note
The verification carried out by Objective CAML as to whether the pattern
matching is exhaustive assumes that the conditional expression in the guard
may be false. Consequently, it does not count this pattern since it is not
possible to know, before execution, whether the guard will be satisfied or
not.
It won't be possible to detect that the pattern matching in the following
example is exhaustive.
# let f = function x when x = x -> true;;
Characters 10-40:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
_
val f : 'a -> bool = <fun>
Pattern matching on character intervals
In the context of pattern matching on characters,
it is tedious to construct the combination of all the patterns
corresponding to a character interval. Indeed, if one wishes to test a
character or even a letter, one would need to write 26 patterns at a
minimum and combine them. For characters, Objective CAML permits writing
patterns of the form:
Syntax
'c1' .. 'cn'
It is equivalent to the combination:
'c1' | 'c2' | ...| 'cn'.
For example the pattern '0' .. '9' corresponds to the pattern
'0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'. The
first form is nicer to read and quicker to write.
Warning
This feature is among the extensions to the language and may change in
future versions.
Using combined patterns and intervals, we define a function categorizing
characters according to several criteria.
# let char_discriminate c = match c with
'a' | 'e' | 'i' | 'o' | 'u' | 'y'
| 'A' | 'E' | 'I' | 'O' | 'U' | 'Y' -> "Vowel"
| 'a'..'z' | 'A'..'Z' -> "Consonant"
| '0'..'9' -> "Digit"
| _ -> "Other" ;;
val char_discriminate : char -> string = <fun>
It should be noted that the order of the groups of patterns has some
significance. Indeed, the second set of patterns includes the first, but
it is not examined until after the check on the first.
Pattern matching on lists
As we have seen, a list can be:
-
either empty (the list is of the form []),
- or composed of a first element (its head) and a sublist (its tail). The
list is then of the form
h
::t.
These two possible ways of writing a list can be used as patterns and allow
pattern matching on a list.
# let rec size x = match x with
[] -> 0
| _::tail_x -> 1 + (size tail_x) ;;
val size : 'a list -> int = <fun>
# size [];;
- : int = 0
# size [7;9;2;6];;
- : int = 4
So we can redo the examples described previously (see page
??) using pattern matching,
such as iteration over lists for example.
# let rec fold_left f a = function
[] -> a
| head::tail -> fold_left f (f a head) tail ;;
val fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a = <fun>
# fold_left (+) 0 [8;4;10];;
- : int = 22
Value declaration through pattern matching
Value declaration in fact uses pattern matching. The declaration
let x = 18 matches the value 18 with the pattern
x. Any pattern is allowed as the left-hand side of a
declaration; the variables in the pattern are bound to the values which
they match.
# let (a,b,c) = (1, true, 'A');;
val a : int = 1
val b : bool = true
val c : char = 'A'
# let (d,c) = 8, 3 in d + c;;
- : int = 11
The scope of pattern variables is the usual static scope for local
declarations. Here, c remains bound to the
value 'A'.
# a + (int_of_char c);;
- : int = 66
As with any kind of pattern matching, value declaration may not be exhaustive.
# let [x;y;z] = [1;2;3];;
Characters 5-12:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
[]
val x : int = 1
val y : int = 2
val z : int = 3
# let [x;y;z] = [1;2;3;4];;
Characters 4-11:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
[]
Uncaught exception: Match_failure("", 4, 11)
Any pattern is allowed, including constructors, wildcards and combined
patterns.
# let head :: 2 :: _ = [1; 2; 3] ;;
Characters 5-19:
Warning: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
[]
val head : int = 1
# let _ = 3. +. 0.14 in "PI" ;;
- : string = "PI"
This last example is of little use in the functional world insofar as
the computed value 3.14 is not named and so is lost.
Type declaration
Type declarations are another possible ingredient in an Objective CAML phrase.
They support the definition of new types corresponding to the original data
structures used in a program. There are two major families of types:
product types for tuples or records; and sum types for
unions.
Type declarations use the keyword type.
Syntax
type name = typedef ;;
In contrast with variable declarations, type declarations are recursive by
default. That is, type declarations, when combined, support the declaration
of mutually recursive types.
Syntax
| type |
name1 |
= |
typedef1 |
| and |
name2 |
= |
typedef2 |
| |
: |
|
|
| and |
namen |
= |
typedefn ;; |
Type declarations can be parameterized by type variables. A type variable
name always begins with an apostrophe
(the ' character):
Syntax
type 'a name = typedef ;;
When there are several of them, the type parameters are declared as a tuple in
front of the name of the type:
Syntax
type
('a1 ...'an)
name = typedef ;;
Only the type parameters defined on the left-hand side of the declaration
may appear on the right-hand side.
Note
Objective CAML's type printer renames the type parameters encountered; the
first is called 'a, the second 'b
and so forth.
One can always define a new type from one or more existing types.
Syntax
type name = type expression
This is useful for constraining a type which one finds too general.
# type 'param paired_with_integer = int * 'param ;;
type 'a paired_with_integer = int * 'a
# type specific_pair = float paired_with_integer ;;
type specific_pair = float paired_with_integer
Nevertheless without type constraints, inference will produce the most
general type.
# let x = (3, 3.14) ;;
val x : int * float = 3, 3.14
But one can use a type constraint to see the desired name appear:
# let (x:specific_pair) = (3, 3.14) ;;
val x : specific_pair = 3, 3.14
Records
Records are tuples, each of whose fields is named in the same way as the
Pascal record or the C struct. A record always
corresponds to the declaration of a new type. A record type is defined by
the declaration of its name and the names and types of each of its fields.
Syntax
type name =
{ name1 : t1;
...; namen : tn
} ;;
We can define a type representing complex numbers by:
# type complex = { re:float; im:float } ;;
type complex = { re: float; im: float }
The creation of a value of record type is done by giving a value to each of
its fields (in arbitrary order).
Syntax
{ namei1 = expri1;
...; namein = exprin
} ;;
For example, we create a complex number with real part
2. and imaginary part 3.:
# let c = {re=2.;im=3.} ;;
val c : complex = {re=2; im=3}
# c = {im=3.;re=2.} ;;
- : bool = true
In the case where some fields are missing, the following error is produced:
# let d = { im=4. } ;;
Characters 9-18:
Some labels are undefined
A field can be accessed in two ways: by the dot notation or by pattern
matching on certain fields.
The dot notation syntax is as usual:
Syntax
expr.name
The expression expr must be of a record type containing a field
name.
Pattern matching a record lets one retrieve the value bound to several
fields. A pattern to match a record has the following syntax:
Syntax
{ namei = pi ;
...; namej = pj }
The patterns are to the right of the = sign (pi, ...,
pj). It is not necessary to make all the fields of a record
appear in such a pattern.
The function add_complex accesses fields through the dot
notation, while the function mult_complex accesses them through
pattern matching.
# let add_complex c1 c2 = {re=c1.re+.c2.re; im=c1.im+.c2.im};;
val add_complex : complex -> complex -> complex = <fun>
# add_complex c c ;;
- : complex = {re=4; im=6}
# let mult_complex c1 c2 = match (c1,c2) with
({re=x1;im=y1},{re=x2;im=y2}) -> {re=x1*.x2-.y1*.y2;im=x1*.y2+.x2*.y1} ;;
val mult_complex : complex -> complex -> complex = <fun>
# mult_complex c c ;;
- : complex = {re=-5; im=12}
The advantages of records, as opposed to tuples, are at least twofold:
-
descriptive and distinguishing information thanks to the field names: in
particular this allows pattern matching to be simplified;
- access in an identical way, by name, to any field of the record
whatsoever: the order of the fields no longer has significance, only their
names count.
The following example shows the ease of accessing the fields of
records as opposed to tuples:
# let a = (1,2,3) ;;
val a : int * int * int = 1, 2, 3
# let f tr = match tr with x,_,_ -> x ;;
val f : 'a * 'b * 'c -> 'a = <fun>
# f a ;;
- : int = 1
# type triplet = {x1:int; x2:int; x3:int} ;;
type triplet = { x1: int; x2: int; x3: int }
# let b = {x1=1; x2=2; x3=3} ;;
val b : triplet = {x1=1; x2=2; x3=3}
# let g tr = tr.x1 ;;
val g : triplet -> int = <fun>
# g b ;;
- : int = 1
For pattern matching, it is not necessary to indicate all the fields of the
record being matched. The inferred type is then that of the last field.
# let h tr = match tr with {x1=x} -> x;;
val h : triplet -> int = <fun>
# h b;;
- : int = 1
There is a construction which lets one create a record identical to
another except for some fields. It is often useful for records containing
many fields.
Syntax
{ name with namei= expri
; ...; namej=exprj}
# let c = {b with x1=0} ;;
val c : triplet = {x1=0; x2=2; x3=3}
A new copy of the value of b is created where only the field
x1 has a new value.
Warning
This feature is among the extensions to the language and may change in
future versions.
Sum types
In contrast with tuples or records, which correspond to a Cartesian
product, the declaration of a sum type corresponds to a union of sets.
Different types (for example integers or character strings) are gathered
into a single type. The various members of the sum are distinguished by
constructors, which support on the one hand, as their name
indicates, construction of values of this type and on the other hand,
thanks to pattern matching, access to the components of these values.
To apply a constructor to an argument is to indicate that the value
returned belongs to this new type.
A sum type is declared by giving the names of its constructors and the
types of their eventual arguments.
Syntax
| type |
name = ... |
| |
| Namei ... |
| |
| Namej of tj ... |
| |
| Namek of tk * ...* tl
...;; |
A constructor name is a particular identifier:
Warning
The names of constructors always begin with a capital letter.
Constant constructors
A constructor which doesn't expect an argument is called a constant
constructor. Constant constructors can subsequently be used directly as a
value in the language, as a constant.
# type coin = Heads | Tails;;
type coin = | Heads | Tails
# Tails;;
- : coin = Tails
The type bool can be defined in this way.
Constructors with arguments
Constructors can have arguments. The keyword of
indicates the type of the constructor's arguments. This supports the
gathering into a single type of objects of different types, each one being
introduced with a particular constructor.
Here is a classic example of defining a datatype to represent the cards in
a game, here Tarot8. The types
suit and card are defined in the following way:
# type suit = Spades | Hearts | Diamonds | Clubs ;;
# type card =
King of suit
| Queen of suit
| Knight of suit
| Knave of suit
| Minor_card of suit * int
| Trump of int
| Joker ;;
The creation of a value of type card is carried out through the
application of a constructor to a value of the appropriate type.
# King Spades ;;
- : card = King Spades
# Minor_card(Hearts, 10) ;;
- : card = Minor_card (Hearts, 10)
# Trump 21 ;;
- : card = Trump 21
And here, for example, is the function all_cards which
constructs a list of all the cards of a suit passed as a parameter.
# let rec interval a b = if a = b then [b] else a::(interval (a+1) b) ;;
val interval : int -> int -> int list = <fun>
# let all_cards s =
let face_cards = [ Knave s; Knight s; Queen s; King s ]
and other_cards = List.map (function n -> Minor_card(s,n)) (interval 1 10)
in face_cards @ other_cards ;;
val all_cards : suit -> card list = <fun>
# all_cards Hearts ;;
- : card list =
[Knave Hearts; Knight Hearts; Queen Hearts; King Hearts;
Minor_card (Hearts, 1); Minor_card (Hearts, 2); Minor_card (Hearts, 3);
Minor_card (Hearts, ...); ...]
To handle values of sum types, we use pattern matching. The following
example constructs conversion functions from values of type suit
and of type card to character strings (type string):
# let string_of_suit = function
Spades -> "spades"
| Diamonds -> "diamonds"
| Hearts -> "hearts"
| Clubs -> "clubs" ;;
val string_of_suit : suit -> string = <fun>
# let string_of_card = function
King c -> "king of " ^ (string_of_suit c)
| Queen c -> "queen of " ^ (string_of_suit c)
| Knave c -> "knave of " ^ (string_of_suit c)
| Knight c -> "knight of " ^ (string_of_suit c)
| Minor_card (c, n) -> (string_of_int n) ^ " of "^(string_of_suit c)
| Trump n -> (string_of_int n) ^ " of trumps"
| Joker -> "joker" ;;
val string_of_card : card -> string = <fun>
Lining up the patterns makes these functions easy to read.
The constructor Minor_card is treated as a constructor with
two arguments. Pattern matching on such a value requires naming
its two components.
# let is_minor_card c = match c with
Minor_card v -> true
| _ -> false;;
Characters 41-53:
The constructor Minor_card expects 2 argument(s),
but is here applied to 1 argument(s)
To avoid having to name each component of a constructor, one declares it to
have a single argument by parenthesizing the corresponding tuple type.
The two constructors which follow are pattern-matched differently.
# type t =
C of int * bool
| D of (int * bool) ;;
# let access v = match v with
C (i, b) -> i,b
| D x -> x;;
val access : t -> int * bool = <fun>
Recursive types
Recursive type definitions are indispensable in any algorithmic language
for describing the usual data structures (lists, heaps, trees, graphs,
etc.). To this end, in Objective CAML type definition is recursive by default,
in contrast with value declaration (let).
Objective CAML's predefined type of lists only takes a single parameter. One may
wish to store values of belonging to two different types in a list
structure, for example, integers (int) or characters
(char). In this case, one defines:
# type int_or_char_list =
Nil
| Int_cons of int * int_or_char_list
| Char_cons of char * int_or_char_list ;;
# let l1 = Char_cons ( '=', Int_cons(5, Nil) ) in
Int_cons ( 2, Char_cons ( '+', Int_cons(3, l1) ) ) ;;
- : int_or_char_list =
Int_cons (2, Char_cons ('+', Int_cons (3, Char_cons ('=', Int_cons (...)))))
Parametrized types
A user can equally well declare types with parameters. This lets us
generalize the example of lists containing values of two different
types.
# type ('a, 'b) list2 =
Nil
| Acons of 'a * ('a, 'b) list2
| Bcons of 'b * ('a, 'b) list2 ;;
# Acons(2, Bcons('+', Acons(3, Bcons('=', Acons(5, Nil))))) ;;
- : (int, char) list2 =
Acons (2, Bcons ('+', Acons (3, Bcons ('=', Acons (...)))))
One can, obviously, instantiate the parameters 'a and
'b with the same type.
# Acons(1, Bcons(2, Acons(3, Bcons(4, Nil)))) ;;
- : (int, int) list2 = Acons (1, Bcons (2, Acons (3, Bcons (4, Nil))))
This use of the type list2 can, as in the preceding example, serve
to mark even integers and odd integers. In this way we extract the sublist
of even integers in order to construct an ordinary list.
# let rec extract_odd = function
Nil -> []
| Acons(_, x) -> extract_odd x
| Bcons(n, x) -> n::(extract_odd x) ;;
val extract_odd : ('a, 'b) list2 -> 'b list = <fun>
The definition of this function doesn't give a single clue as to the nature
of the values stored in the structure. That is why its type is
parameterized.
Scope of declarations
Constructor names obey the same scope discipline as global declarations: a
redefinition masks the previous one. Nevertheless values of the masked
type still exist. The interactive toplevel does not distinguish these two
types in its output. Whence some unclear error messages.
In this first example, the constant constructor Nil of type
int_or_char has been masked by the constructor declarations of
the type ('a, 'b) list2.
# Int_cons(0, Nil) ;;
Characters 13-16:
This expression has type ('a, 'b) list2 but is here used with type
int_or_char_list
This second example provokes a rather baffling error message, at least the
first time it appears. Let the little program be as follows:
# type t1 = Empty | Full;;
type t1 = | Empty | Full
# let empty_t1 x = match x with Empty -> true | Full -> false ;;
val empty_t1 : t1 -> bool = <fun>
# empty_t1 Empty;;
- : bool = true
Then, we redeclare the type t1:
# type t1 = {u : int; v : int} ;;
type t1 = { u: int; v: int }
# let y = { u=2; v=3 } ;;
val y : t1 = {u=2; v=3}
Now if we apply the function empty_t1 to a value of the new type
t1, we get the following error message:
# empty_t1 y;;
Characters 10-11:
This expression has type t1 but is here used with type t1
The first occurrence of t1 represents the first type defined, while
the second corresponds to the second type.
Function types
The type of the argument of a constructor may be arbitrary. In particular,
it may very well contain a function type. The following type constructs
lists, all of whose elements except the last are function values.
# type 'a listf =
Val of 'a
| Fun of ('a -> 'a) * 'a listf ;;
type 'a listf = | Val of 'a | Fun of ('a -> 'a) * 'a listf
Since function values are values which can be manipulated in the language,
we can construct values of type listf:
# let eight_div = (/) 8 ;;
val eight_div : int -> int = <fun>
# let gl = Fun (succ, (Fun (eight_div, Val 4))) ;;
val gl : int listf = Fun (<fun>, Fun (<fun>, Val 4))
and functions which pattern-match such values:
# let rec compute = function
Val v -> v
| Fun(f, x) -> f (compute x) ;;
val compute : 'a listf -> 'a = <fun>
# compute gl;;
- : int = 3
Example: representing trees
Tree structures come up frequently in programming. Recursive types make it
easy to define and manipulate such structures. In this subsection, we give two
examples of tree structures.
Binary trees
We define a binary tree structure whose nodes are labelled with values of a
single type by declaring:
# type 'a bin_tree =
Empty
| Node of 'a bin_tree * 'a * 'a bin_tree ;;
We use this structure to define a little sorting program using binary
search trees. A binary search tree has the property that all the values in
the left branch are less than that of the root, and all those of the right
branch are greater. Figure 2.5 gives an example of such a
structure over the integers. The empty nodes (constructor Empty)
are represented there by little squares; the others (constructor
Node), by a circle in which is inscribed the stored value.
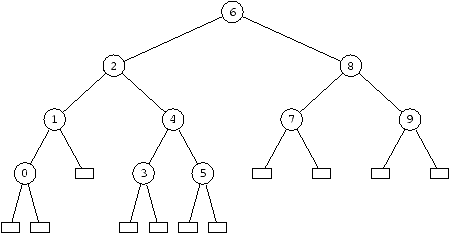
Figure 2.5: Binary search tree.
A sorted list is extracted from a binary search tree via an inorder
traversal carried out by the following function:
# let rec list_of_tree = function
Empty -> []
| Node(lb, r, rb) -> (list_of_tree lb) @ (r :: (list_of_tree rb)) ;;
val list_of_tree : 'a bin_tree -> 'a list = <fun>
To obtain a binary search tree from a list, we define an insert function.
# let rec insert x = function
Empty -> Node(Empty, x, Empty)
| Node(lb, r, rb) -> if x < r then Node(insert x lb, r, rb)
else Node(lb, r, insert x rb) ;;
val insert : 'a -> 'a bin_tree -> 'a bin_tree = <fun>
The function to transform a list into a tree is obtained by iterating the
function insert.
# let rec tree_of_list = function
[] -> Empty
| h::t -> insert h (tree_of_list t) ;;
val tree_of_list : 'a list -> 'a bin_tree = <fun>
The sort function is then simply the composition of the functions
tree_of_list and list_of_tree.
# let sort x = list_of_tree (tree_of_list x) ;;
val sort : 'a list -> 'a list = <fun>
# sort [5; 8; 2; 7; 1; 0; 3; 6; 9; 4] ;;
- : int list = [0; 1; 2; 3; 4; 5; 6; 7; 8; 9]
General planar trees
In this part, we use the following predefined functions from the
List module (see page ??):
-
List.map: which applies a function to all the elements of a
list and returns the list of results;
- List.fold_left: which is an equivalent version of the
function fold_left defined on page ??;
- List.exists: which applies a boolean-valued function to all
the elements of a list; if one of these applications yields true
then the result is true, otherwise the function returns
false.
A general planar tree is a tree whose number of branches is not
fixed a priori; to each node is associated a list of branches whose
length may vary.
# type 'a tree = Empty
| Node of 'a * 'a tree list ;;
The empty tree is represented by the value Empty. A leaf is a node
without branches either of the form Node(x,[]), or of the
degenerate form Node(x, [Empty;Empty; ..]). It is then relatively
easy to write functions to manipulate these trees, e.g., to determine
whether an element belongs to a tree or compute the height of the tree.
To test membership of an element e, we use the following
algorithm: if the tree is empty then e does not belong to this
tree, otherwise e belongs to the tree if and only if either it is
equal to the label of the root, or it belongs to one of its branches.
# let rec belongs e = function
Empty -> false
| Node(v, bs) -> (e=v) or (List.exists (belongs e) bs) ;;
val belongs : 'a -> 'a tree -> bool = <fun>
To compute the height of a tree, we use the following definition: an empty
tree has height 0, otherwise the height of the tree is equal to
the height of its highest subtree plus 1.
# let rec height =
let max_list l = List.fold_left max 0 l in
function
Empty -> 0
| Node (_, bs) -> 1 + (max_list (List.map height bs)) ;;
val height : 'a tree -> int = <fun>
Recursive values which are not functions
Recursive declaration of non-function values allows the construction of
circular data structures.
The following declaration constructs a circular list with one element.
# let rec l = 1::l ;;
val l : int list =
[1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; ...]
Application of a recursive function to such a list risks looping until
memory overflows.
# size l ;;
Stack overflow during evaluation (looping recursion?).
Structural equality remains usable with such lists only when physical
equality is first verified:
# l=l ;;
- : bool = true
In short, if you define a new list, even an equal one, you must not use the
structural equality test on pain of seeing your program loop indefinitely.
So we don't recommend attempting to evaluate the following example:
let rec l2 = 1::l2 in l=l2 ;;
On the other hand, physical equality always remains possible.
# let rec l2 = 1::l2 in l==l2 ;;
- : bool = false
The predicate == tests equality of an immediate value or sharing
of a structured object (equality of the address of the value). We will use
it to verify that in traversing a list we don't retraverse a sublist which
was already examined. First of all, we define the function memq,
which verifies the presence of an element in the list by relying on
physical equality. It is the counterpart to the function mem
which tests structural equality; these two functions belong to the module
List.
# let rec memq a l = match l with
[] -> false
| b::l -> (a==b) or (memq a l) ;;
val memq : 'a -> 'a list -> bool = <fun>
The size computation function is redefined, storing the list of lists
already examined and halting if a list is encountered a second time.
# let special_size l =
let rec size_aux previous l = match l with
[] -> 0
| _::l1 -> if memq l previous then 0
else 1 + (size_aux (l::previous) l1)
in size_aux [] l ;;
val special_size : 'a list -> int = <fun>
# special_size [1;2;3;4] ;;
- : int = 4
# special_size l ;;
- : int = 1
# let rec l1 = 1::2::l2 and l2 = 1::2::l1 in special_size l1 ;;
- : int = 4








