Previous Contents Next

Mixing Styles

As we have mentioned, a language offering both functional and imperative characteristics allows the programmer to choose the more appropriate style for each part of the implementation of an algorithm. One can indeed use both aspects in the same function. This is what we will now illustrate.

Closures and Side Effects

The convention, when a function causes a side effect, is to treat it as a procedure and to return the value (), of type unit. Nevertheless, in some cases, it can be useful to cause the side effect within a function that returns a useful value. We have already used this mixture of the styles in the function permute_pivot of quicksort.

The next example is a symbol generator that creates a new symbol each time that it is called. It simply uses a counter that is incremented at every call. 

# let c = ref 0;;
val c : int ref = {contents=0}
# let reset_symb = function () -> c:=0 ;;
val reset_symb : unit -> unit = <fun>
# let new_symb = function s ->  c:=!c+1 ; s^(string_of_int !c) ;;
val new_symb : string -> string = <fun>
# new_symb "VAR" ;;
- : string = "VAR1"
# new_symb "VAR" ;;
- : string = "VAR2"
# reset_symb () ;;
- : unit = ()
# new_symb "WAR" ;;
- : string = "WAR1"
# new_symb "WAR" ;;
- : string = "WAR2"


The reference c may be hidden from the rest of the program by writing: 

# let (reset_s , new_s) = 
   let c = ref 0 
   in let f1 () = c := 0  
      and f2 s  = c := !c+1 ; s^(string_of_int !c) 
   in (f1,f2) ;;
val reset_s : unit -> unit = <fun>
val new_s : string -> string = <fun>


This declaration creates a pair of functions that share the variable c, which is local to this declaration. Using these two functions produces the same behavior as the previous definitions. 

# new_s "VAR";;
- : string = "VAR1"
# new_s "VAR";;
- : string = "VAR2"
# reset_s();;
- : unit = ()
# new_s "WAR";;
- : string = "WAR1"
# new_s "WAR";;
- : string = "WAR2"


This example permits us to illustrate the way that closures are represented. A closure may be considered as a pair containing the code (that is, the function part) as one component and the local envoronment containing the values of the free variables of the function. Figure 4.1 shows the memory representation of the closures reset_s and new_s.



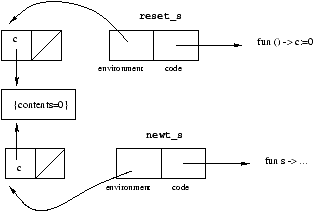
Figure 4.1: Memory representation of closures.

These two closures share the same environment, containing the value of c. When either one modifies the reference c, it modifies the contents of an area of memory that is shared with the other closure.

Physical Modifications and Exceptions

Exceptions make it possible to escape from situations in which the computation cannot proceed. In this case, an exception handler allows the calculation to continue, knowing that one branch has failed. The problem with side effects comes from the state of the modifiable data when the exception was raised. One cannot be sure of this state if there have been physical modifications in the branch of the calculation that has failed.

Let us define the increment function (++) analogous to the operator in C: 

# let (++) x = x:=!x+1; x;;
val ++ : int ref -> int ref = <fun>
The following example shows a little computation where division by zero occurs together with 

# let x = ref 2;;
val x : int ref = {contents=2}
(* 1 *)
# !((++) x) * (1/0) ;;
Uncaught exception: Division_by_zero
# x;;
- : int ref = {contents=2}
(* 2 *)
# (1/0) * !((++) x) ;;
Uncaught exception: Division_by_zero
# x;;
- : int ref = {contents=3}
The variable x is not modified during the computation of the expression in (*1*), while it is modified in the computation of (*2*). Unless one saves the initial values, the form try .. with .. must not have a with .. part that depends on modifiable variables implicated in the expression that raised the exception.

Modifiable Functional Data Structures

In functional programming a program (in particular, a function expression) may also serve as a data object that may be manipulated, and one way to see this is to write association lists in the form of function expressions. In fact, one may view association lists of type ('a * 'b) list as partial functions taking a key chosen from the set 'a and returning a value in the set of associated values 'b. Each association list is then a function of type 'a -> 'b.

The empty list is the everywhere undefined function, which one simulates by raising an exception: 

# let nil_assoc = function x -> raise Not_found ;;
val nil_assoc : 'a -> 'b = <fun>


We next write the function add_assoc which adds an element to a list, meaning that it extends the function for a new entry: 

# let add_assoc (k,v) l = function x -> if x = k then v else l x ;;
val add_assoc : 'a * 'b -> ('a -> 'b) -> 'a -> 'b = <fun>
# let l = add_assoc ('1', 1) (add_assoc ('2', 2) nil_assoc) ;;
val l : char -> int = <fun>
# l '2' ;;
- : int = 2
# l 'x' ;;
Uncaught exception: Not_found


We may now re-write the function mem_assoc: 

# let mem_assoc k l = try  (l k) ; true  with  Not_found -> false ;;
val mem_assoc : 'a -> ('a -> 'b) -> bool = <fun>
# mem_assoc '2' l ;;
- : bool = true
# mem_assoc 'x' l ;;
- : bool = false


By contrast, writing a function to remove an element from a list is not trivial, because one no longer has access to the values captured by the closures. To accomplish the same purpose we mask the former value by raising the exception Not_found. 

# let rem_assoc k l = function x -> if x=k then raise Not_found else l x ;;
val rem_assoc : 'a -> ('a -> 'b) -> 'a -> 'b = <fun>
# let l = rem_assoc '2' l ;;
val l : char -> int = <fun>
# l '2' ;;
Uncaught exception: Not_found


Clearly, one may also create references and work by side effect on such values. However, one must take some care. 

# let add_assoc_again (k,v) l =  l := (function x -> if x=k then v else !l x) ;;
val add_assoc_again : 'a * 'b -> ('a -> 'b) ref -> unit = <fun>


The resulting value for l is a function that points at itself and therefore loops. This annoying side effect is due to the fact that the dereferencing !l is within the scope of the closure function x ->. The value of !l is not evaluated during compilation, but at run-time. At that time, l points to the value that has already been modified by add_assoc. We must therefore correct our definition using the closure created by our original definition of add_assoc: 

# let add_assoc_again (k, v) l =  l := add_assoc (k, v) !l ;;
val add_assoc_again : 'a * 'b -> ('a -> 'b) ref -> unit = <fun>
# let l = ref nil_assoc ;;
val l : ('_a -> '_b) ref = {contents=<fun>}
# add_assoc_again ('1',1) l ;;
- : unit = ()
# add_assoc_again ('2',2) l ;;
- : unit = ()
# !l '1' ;;
- : int = 1
# !l 'x' ;;
Uncaught exception: Not_found


Lazy Modifiable Data Structures

Combining imperative characteristics with a functional language produces good tools for implementing computer languages. In this subsection, we will illustrate this idea by implementing data structures with deferred evaluation. A data structure of this kind is not completely evaluated. Its evaluation progresses according to the use made of it.

Deferred evaluation, which is often used in purely functional languages, is simulated using function values, possibly modifiable. There are at least two purposes for manipulating incompletely evaluated data structures: first, so as to calculate only what is effectively needed in the computation; and second, to be able to work with potentially infinite data structures.

We define the type vm, whose members contain either an already calculated value (constructor Imm) or else a value to be calculated (constructor Deferred): 

# type 'a v = 
     Imm of 'a
   | Deferred of (unit -> 'a);;
# type 'a vm = {mutable c : 'a v };;


A computation is deferred by encapsulating it in a closure. The evaluation function for deferred values must return the value if it has already been calculated, and otherwise, if the value is not already calculated, it must evaluate it and then store the result. 

# let eval e = match e.c with 
   Imm a -> a
 | Deferred f -> let u = f () in e.c <- Imm u ; u ;;
val eval : 'a vm -> 'a = <fun>


The operations of deferring evaluation and activating it are also called freezing and thawing a value.

We could also write the conditional control structure in the form of a function: 

# let if_deferred c e1 e2 = 
   if eval c then eval e1 else eval e2;;
val if_deferred : bool vm -> 'a vm -> 'a vm -> 'a = <fun>


Here is how to use it in a recursive function such as factorial: 

# let rec facr n = 
   if_deferred
          {c=Deferred(fun () -> n = 0)} 
          {c=Deferred(fun () ->  1)} 
          {c=Deferred(fun () -> n*(facr(n-1)))};;
val facr : int -> int = <fun>
# facr 5;;
- : int = 120


The classic form of if can not be written in the form of a function. In fact, if we define a function if_function this way: 

# let if_function c e1 e2 = if c then e1 else e2;;
val if_function : bool -> 'a -> 'a -> 'a = <fun>


then the three arguments of if_function are evaluated at the time they are passed to the function. So the function fact loops, because the recursive call fact(n-1) is always evaluated, even when n has the value 0. 

# let rec fact n = if_function (n=0) 1 (n*fact(n-1)) ;;
val fact : int -> int = <fun>
# fact 5 ;;
Stack overflow during evaluation (looping recursion?).


Module Lazy

The implementation difficulty for frozen values is due to the conflict between the eager evaluation strategy of Objective CAML and the need to leave expressions unevaluated. Our attempt to redefine the conditional illustrated this. More generally, it is impossible to write a function that freezes a value in producing an object of type vm: 

# let freeze e = { c = Deferred (fun () -> e) };;
val freeze : 'a -> 'a vm = <fun>
When this function is applied to arguments, the Objective CAML evaluation strategy evaluates the expression e passed as argument before constructing the closure fun () -> e. The next example shows this: 

# freeze (print_string "trace"; print_newline(); 4*5);;
trace
- : int vm = {c=Deferred <fun>}


This is why the following syntactic form was introduced.

Syntax

lazy expr


Warning

This form is a language extension that may evolve in future versions.


When the keyword lazy is applied to an expression, it constructs a value of a type declared in the module Lazy: 

# let x = lazy (print_string "Hello"; 3*4) ;;
val x : int Lazy.status ref = {contents=Lazy.Delayed <fun>}


The expression (print_string "Hello") has not been evaluated, because no message has been printed. The function force of module Lazy allows one to force evaluation: 

# Lazy.force x ;;
Hello- : int = 12
Now the value x has altered: 

# x ;;
- : int Lazy.t = {contents=Lazy.Value 12}
It has become the value of the expression that had been frozen, namely 12.

For another call to the function force, it's enough to return the value already calculated: 

# Lazy.force x ;;
- : int = 12
The string "Hello" is no longer prefixed.

``Infinite'' Data Structures

The second reason to defer evaluation is to be able to construct potentially infinite data structures such as the set of natural numbers. Because it might take a long time to construct them all, the idea here is to compute only the first one and to know how to pass to the next element.

We define a generic data structure 'a enum which will allow us to enumerate the elements of a set. 

# type 'a enum = { mutable i : 'a; f :'a -> 'a } ;;
type 'a enum = { mutable i: 'a; f: 'a -> 'a }
# let next e = let x = e.i in e.i <- (e.f e.i) ; x ;;
val next : 'a enum -> 'a = <fun>


Now we can get the set of natural numbers by instantiating the fields of this structure: 

# let nat = { i=0; f=fun x -> x + 1 };;
val nat : int enum = {i=0; f=<fun>}
# next nat;;
- : int = 0
# next nat;;
- : int = 1
# next nat;;
- : int = 2
Another example gives the elements of the Fibonnacci sequence, which has the definition:
ì
í
î
u0 = 1
u1 = 1
un+2 = un + un+1
The function to compute the successor must take account of the current value, (un-1), but also of the preceding one (un-2). For this, we use the state c in the following closure: 

# let fib = let fx = let c = ref 0 in fun v -> let r = !c + v in c:=v ; r
           in { i=1 ; f=fx } ;;
val fib : int enum = {i=1; f=<fun>}
# for i=0 to 10 do  print_int (next fib); print_string "  " done ;;
1  1  2  3  5  8  13  21  34  55  89  - : unit = ()


Previous Contents Next