Types and Genericity

Types and Genericity

Besides the ability to model a problem using aggregation and inheritance relations, object-oriented programming is interesting because it provides the ability to reuse or modify the behavior of classes. However, extending an Objective CAML class must preserve the static typing properties of the language.

With abstract classes, you can factorize code and group their subclasses into one ``communication protocol''. An abstract class fixes the names and types of messages that may be received by instances of child classes. This technique will be better appreciated in connection with multiple inheritance.

The notion of an open object type (or simply an open type) that specifies the required methods allows code to work with instances using generic functions. But you may need to make the type constraints precise; this will be necessary for parameterized classes, which provide the genericity of parameterized polymorphism in the context of classes. With this latter object layer feature, Objective CAML can really be generic.

Abstract Classes and Methods

In abstract classes, some methods are declared without a body. Such methods are called abstract. It is illegal to instantiate an abstract class; new cannot be used. The keyword virtual is used to indicate that a class or method is abstract.

Syntax

class virtual name = object ...end

A class must be declared abstract as soon as one of its methods is abstract. A method is declared abstract by providing only the method type.

Syntax

method virtual name : type

When a subclass of an abstract class redefines all of the abstract methods of its parent, then it may become concrete; otherwise it also has to be declared abstract.

As an example, suppose we want to construct a set of displayable objects, all with a method print that will display the object's contents translated into a character string. All such objects need a method to_string. We define class printable. The string may vary according to the nature of the objects that we consider; therefore method to_string is abstract in the declaration of printable and consequently the class is also abstract.


# class virtual printable () =
   object(self)
     method virtual to_string : unit -> string
     method print () = print_string (self#to_string())
   end ;;
class virtual printable :
  unit ->
  object
    method print : unit -> unit
    method virtual to_string : unit -> string
  end

We note that the abstractness of the class and of its method to_string is made clear in the type we obtain.

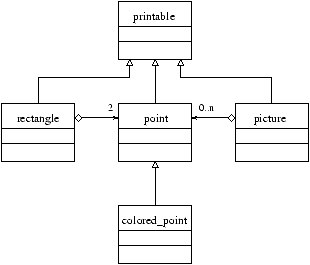
From this class, let us try to define the class hierarchy of figure 15.4.

Figure 15.4: Relations between classes of displayable objects.

It is easy to redefine the classes point, colored_point and picture by adding to their declarations a line inherit printable () that provides them with a method print through inheritance.


# let p = new point (1,1) in p#print() ;;
( 1, 1)- : unit = ()
# let pc = new colored_point (2,2) "blue" in pc#print() ;;
( 2, 2) with color blue- : unit = ()
# let t = new picture 3 in t#add (new point (1,1)) ; 
                          t#add (new point (3,2)) ; 
                          t#add (new point (1,4)) ;
                          t#print() ;;
[ ( 1, 1) ( 3, 2) ( 1, 4)]- : unit = ()

Subclass rectangle below inherits from printable, and defines method to_string. Instance variables llc (resp. urc) mean the lower left corner point (resp. upper right corner point) in the rectangle.


# class rectangle (p1,p2) = 
   object
     inherit printable ()
     val llc = (p1 : point)
     val urc = (p2 : point)
     method to_string () = "[" ^ llc#to_string() ^ "," ^ urc#to_string() ^ "]"
   end ;;
class rectangle :
  point * point ->
  object
    val llc : point
    val urc : point
    method print : unit -> unit
    method to_string : unit -> string
  end

Class rectangle inherits from the abstract class printable, and thus receives method print. It has two instance variables of type point: the lower left corner (llc) and upper right corner. Method to_string sends the message to_string to its point instance variables llc and urc.


# let r = new rectangle (new point (2,3), new point (4,5));;
val r : rectangle = <obj>
# r#print();;
[( 2, 3),( 4, 5)]- : unit = ()

Classes, Types, and Objects

You may remember that the type of an object is determined by the type of its methods. For instance, the type point, inferred during the declaration of class point, is an abbreviation for type:

  point =
    < distance : unit -> float; get_x : int; get_y : int;
      moveto : int * int -> unit; rmoveto : int * int -> unit;
      to_string : unit -> string  >

This is a closed type; that is, all methods and associated types are fixed. No additional methods and types are allowed. Upon a class declaration, the mechanism of type inference computes the closed type associated with class.

Open Types

Since sending a message to an object is part of the language, you may define a function that sends a message to an object whose type is still undefined.


# let f x = x#get_x ;;
val f : < get_x : 'a; .. > -> 'a = <fun>

The type inferred for the argument of f is an object type, since a message is sent to x, but this object type is open. In function f, parameter x must have at least a method get_x. Since the result of sending this message is not used within function f, its type has to be as general as possible (i.e. a variable of type 'a). So type inference allows the function f to be used with any object having a method get_x. The double points (..) at the end of the type < get_x : 'a; .. > indicate that the type of x is open.


# f (new point(2,3)) ;;
- : int = 2
# f (new colored_point(2,3) "emerald") ;;
- : int = 2
# class c () =
   object
     method get_x = "I have a method get_x" 
   end ;;
class c : unit -> object method get_x : string end
# f (new c ()) ;;
- : string = "I have a method get_x"

Type inference for classes may generate open types, particularly for initial values in instance construction. The following example constructs a class couple, whose initial values a and b have a method to_string.


# class couple (a,b) =
   object
     val p0 = a
     val p1 = b
     method to_string() = p0#to_string() ^ p1#to_string()
     method copy () = new couple (p0,p1)
   end ;;
class couple :
  (< to_string : unit -> string; .. > as 'a) *
  (< to_string : unit -> string; .. > as 'b) ->
  object
    val p0 : 'a
    val p1 : 'b
    method copy : unit -> couple
    method to_string : unit -> string
  end

The types of both a and b are open types, with method to_string. We note that these two types are considered to be different. They are marked ``as 'a'' and ``as 'b'', respectively. Variables of types 'a and 'b are constrained by the generated type.

We use the sharp symbol to indicate the open type built from a closed type obj_type:

Syntax

#obj_type

The type obtained contains all of the methods of type obj_type and terminates with a double point.

Type Constraints.

In the chapter on functional programming (see page ??), we showed how an expression can be constrained to have a type more precise than what is produced by inference. Object types (open or closed) can be used to enhance such constraints. One may want to open a priori the type of a defined object, in order to apply it to a forthcoming method. We can use an open object constraint:

Syntax

(name:#type)

Which allows us to write:


# let g (x : #point) = x#message;;
val g :
  < distance : unit -> float; get_x : int; get_y : int; message : 'a;
    moveto : int * int -> unit; print : unit -> unit;
    rmoveto : int * int -> unit; to_string : unit -> string; .. > ->
  'a = <fun>

The type constraint with #point forces x to have at least all of the methods of point, and sending message ``message'' adds a method to the type of parameter x.

Just as in the rest of the language, the object extension of Objective CAML provides static typing through inference. When this mechanism does not have enough information to determine the type of an expression, a type variable is assigned. We have just seen that this process is also valid for typing objects; however, it sometimes leads to ambiguous situations which the user must resolve by explicitly giving type information.


# class a_point p0 =
   object
     val p = p0
     method to_string() = p#to_string() 
   end ;;
Characters 6-89:
Some type variables are unbound in this type:
  class a_point :
    (< to_string : unit -> 'b; .. > as 'a) ->
    object val p : 'a method to_string : unit -> 'b end
The method to_string has type unit -> 'a where 'a is unbound

We resolve this ambiguity by saying that parameter p0 has type #point.


# class a_point (p0 : #point) =
   object
     val p = p0
     method to_string() = p#to_string()
   end ;;
class a_point :
  (#point as 'a) -> object val p : 'a method to_string : unit -> string end

In order to set type constraints in several places in a class declaration, the following syntax is used:

Syntax

constraint type₁ = type₂

The above example can be written specifying that parameter p0 has type 'a, then putting a type constraint upon variable 'a.


# class a_point (p0 : 'a) =
   object
     constraint 'a = #point
     val p = p0
     method to_string() = p#to_string()
   end ;;
class a_point :
  (#point as 'a) -> object val p : 'a method to_string : unit -> string end

Several type constraints can be given in a class declaration.

Warning

An open type cannot appear as the type of a method.

This strong restriction exists because an open type contains an uninstantiated type variable coming from the rest of the type. Since one cannot have a free variable type in a type declaration, a method containing such a type is rejected by type inference.


# class b_point p0  =
   object
     inherit a_point p0
     method get = p
   end ;;
Characters 6-77:
Some type variables are unbound in this type:
  class b_point :
    (#point as 'a) ->
    object val p : 'a method get : 'a method to_string : unit -> string end
The method get has type #point where .. is unbound

In fact, due to the constraint ``constraint 'a = #point'', the type of get is the open type #point. The latter contains a free variable type noted by a double point (..), which is not allowed.

Inheritance and the Type of `self`

There exists an exception to the prohibition of a type variable in the type of methods: a variable may stand for the type of the object itself (self). Consider a method testing the equality between two points.


# class point_eq (x,y) = 
   object (self : 'a) 
     inherit point (x,y)
     method eq (p:'a) = (self#get_x = p#get_x) && (self#get_y = p#get_y)
   end ;;
class point_eq :
  int * int ->
  object ('a)
    val mutable x : int
    val mutable y : int
    method distance : unit -> float
    method eq : 'a -> bool
    method get_x : int
    method get_y : int
    method moveto : int * int -> unit
    method print : unit -> unit
    method rmoveto : int * int -> unit
    method to_string : unit -> string
  end

The type of method eq is 'a -> bool, but the type variable stands for the type of the instance at construction time.

You can inherit from the class point_eq and redefine the method eq, whose type is still parameterized by the instance type.


# class colored_point_eq (xc,yc) c = 
   object (self : 'a) 
     inherit point_eq (xc,yc) as super 
     val c = (c:string)
     method get_c = c
     method eq (pc : 'a) =  (self#get_x = pc#get_x) && (self#get_y = pc#get_y) 
                         && (self#get_c = pc#get_c)
   end ;;
class colored_point_eq :
  int * int ->
  string ->
  object ('a)
    val c : string
    val mutable x : int
    val mutable y : int
    method distance : unit -> float
    method eq : 'a -> bool
    method get_c : string
    method get_x : int
    method get_y : int
    method moveto : int * int -> unit
    method print : unit -> unit
    method rmoveto : int * int -> unit
    method to_string : unit -> string
  end

The method eq from class colored_point_eq still has type 'a -> bool; but now the variable 'a stands for the type of an instance of class colored_point_eq. The definition of eq in class colored_point_eq masks the inherited one. Methods containing the type of the instance in their type are called binary methods. They will cause some limitations in the subtyping relation described in page ??.

Multiple Inheritance

With multiple inheritance, you can inherit data fields and methods from several classes. When there are identical names for fields or methods, only the last declaration is kept, according to the order of inheritance declarations. Nevertheless, it is possible to reference a method of one of the parent classes by associating different names with the inherited classes. This is not true for instance variables: if an inherited class masks an instance variable of a previously inherited class, the latter is no longer directly accessible. The various inherited classes do not need to have an inheritance relation. Multiple inheritance is of interest because it increases class reuse.

Let us define the abstract class geometric_object, which declares two virtual methods compute_area and compute_peri for computing the area and perimeter.


# class virtual geometric_object () =
 object
   method virtual compute_area : unit -> float
   method virtual compute_peri : unit -> float
 end;;

Then we redefine class rectangle as follows:


# class rectangle_1 ((p1,p2) :'a) = 
 object
   constraint 'a = point * point
   inherit printable ()
   inherit geometric_object ()
   val llc = p1
   val urc = p2
   method to_string () = 
    "["^llc#to_string()^","^urc#to_string()^"]"
   method compute_area() = 
    float ( abs(urc#get_x - llc#get_x) * abs(urc#get_y - llc#get_y))
   method compute_peri() = 
    float ( (abs(urc#get_x - llc#get_x) + abs(urc#get_y - llc#get_y)) * 2)
 end;;
class rectangle_1 :
  point * point ->
  object
    val llc : point
    val urc : point
    method compute_area : unit -> float
    method compute_peri : unit -> float
    method print : unit -> unit
    method to_string : unit -> string
  end

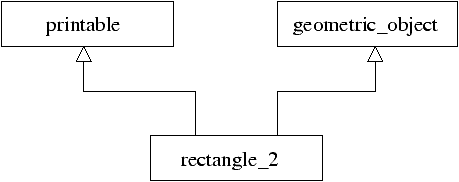
This implementation of classes respects the inheritance graph of figure 15.5.

Figure 15.5: Multiple inheritance.

In order to avoid rewriting the methods of class rectangle, we may directly inherit from rectangle, as shown in figure 15.6.

Figure 15.6: Multiple inheritance (continued).

In such a case, only the abstract methods of the abstract class geometric_object must be defined in rectangle_2.


# class rectangle_2 (p2 :'a) = 
   object
   constraint 'a = point * point
   inherit rectangle p2 
   inherit geometric_object () 
   method compute_area() = 
    float ( abs(urc#get_x - llc#get_x) * abs(urc#get_y - llc#get_y))
   method compute_peri() = 
    float ( (abs(urc#get_x - llc#get_x) + abs(urc#get_y - llc#get_y)) * 2)
 end;;

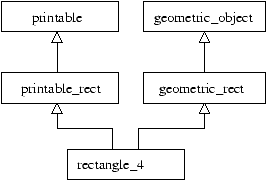
Continuing in the same vein, the hierarchies printable and geometric_object could have been defined separately, until it became useful to have a class with both behaviors. Figure 15.7 displays the relations defined in this way.

Figure 15.7: Multiple inheritance (end).

If we assume that classes printable_rect and geometric_rect define instance variables for the corners of a rectangle, we get class rectangle_3 with four points (two per corner).


class rectangle_3 (p1,p2) =
 inherit printable_rect (p1,p2) as super_print
 inherit geometric_rect (p1,p2) as super_geo
end;;

In the case where methods of the same type exist in both classes ..._rect, then only the last one is visible. However, by naming parent classes (super_...), it is always possible to invoke a method from either parent.

Multiple inheritance allows factoring of the code by integrating methods already written from various parent classes to build new entities. The price paid is the size of constructed objects, which are bigger than necessary due to duplicated fields, or inherited fields useless for a given application. Furthermore, when there is duplication (as in our last example), communication between these fields must be established manually (update, etc.). In the last example for class rectangle_3, we obtain instance variables of classes printable_rect and geometric_rect. If one of these classes has a method which modifies these variables (such as a scaling factor), then it is necessary to propagate these modifications to variables inherited from the other class. Such a heavy communication between inherited instance variables often signals a poor modeling of the given problem.

Parameterized Classes

Parameterized classes let Objective CAML's parameterized polymorphism be used in classes. As with the type declarations of Objective CAML, class declarations can be parameterized with type variables. This provides new opportunities for genericity and code reuse. Parameterized classes are integrated with ML-like typing when type inference produces parameterized types.

The syntax differs slightly from the declaration of parameterized types; type parameters are between brackets.

Syntax

class ['a, 'b, ...] name = object ...end

The Objective CAML type is noted as usual: ('a,'b,...) name.

For instance, if a class pair is required, a naive solution would be to set:


# class pair x0 y0 =
   object
     val x = x0    
     val y = y0
     method fst = x
     method snd = y
   end ;;        
Characters 6-106:
Some type variables are unbound in this type:
  class pair :
    'a ->
    'b -> object val x : 'a val y : 'b method fst : 'a method snd : 'b end
The method fst has type 'a where 'a is unbound

One again gets the typing error mentioned when class a_point was defined (page ??). The error message says that type variable 'a, assigned to parameter x0 (and therefore to x and fst), is not bound.

As in the case of parameterized types, it is necessary to parameterize class pair with two type variables, and force the type of construction parameters x0 and y0 to obtain a correct typing:


# class ['a,'b] pair (x0:'a) (y0:'b) =
   object
     val x = x0
     val y = y0
     method fst = x
     method snd = y
   end ;;
class ['a, 'b] pair :
  'a ->
  'b -> object val x : 'a val y : 'b method fst : 'a method snd : 'b end

Type inference displays a class interface parameterized by variables of type 'a and 'b.

When a value of a parameterized class is constructed, type parameters are instantiated with the types of the construction parameters:


# let p = new pair 2 'X';;
val p : (int, char) pair = <obj>
# p#fst;;
- : int = 2
# let q = new pair 3.12 true;;
val q : (float, bool) pair = <obj>
# q#snd;;
- : bool = true

Note

In class declarations, type parameters are shown between brackets, but in types, they are shown between parentheses.

Inheritance of Parameterized Classes

When inheriting from a parameterized class, one has to indicate the parameters of the class. Let us define a class acc_pair that inherits from ('a,'b) pair; we add two methods for accessing the fields, get1 and get2,


# class ['a,'b] acc_pair (x0 : 'a) (y0 : 'b) = 
   object
     inherit ['a,'b] pair x0 y0 
     method get1 z = if x = z then y else raise Not_found
     method get2 z = if y = z then x else raise Not_found
   end;;
class ['a, 'b] acc_pair :
  'a ->
  'b ->
  object
    val x : 'a
    val y : 'b
    method fst : 'a
    method get1 : 'a -> 'b
    method get2 : 'b -> 'a
    method snd : 'b
  end
# let p = new acc_pair 3 true;;
val p : (int, bool) acc_pair = <obj>
# p#get1 3;;
- : bool = true

We can make the type parameters of the inherited parameterized class more precise, e.g. for a pair of points.


# class point_pair (p1,p2) = 
   object
     inherit [point,point] pair p1 p2
   end;;
class point_pair :
  point * point ->
  object
    val x : point
    val y : point
    method fst : point
    method snd : point
  end

Class point_pair no longer needs type parameters, since parameters 'a and 'b are completely determined.

To build pairs of displayable objects (i.e. having a method print), we reuse the abstract class printable (see page ??), then we define the class printable_pair which inherits from pair.


# class printable_pair x0 y0 = 
   object
     inherit [printable, printable] acc_pair x0 y0
     method print () = x#print(); y#print ()
   end;;

This implementation allows us to construct pairs of instances of printable, but it cannot be used for objects of another class with a method print.

We could try to open type printable used as a type parameter for acc_pair:


# class printable_pair (x0 ) (y0 ) = 
   object
     inherit [ #printable, #printable ] acc_pair x0 y0
     method print () = x#print(); y#print ()
   end;;
Characters 6-149:
Some type variables are unbound in this type:
  class printable_pair :
    (#printable as 'a) ->
    (#printable as 'b) ->
    object
      val x : 'a
      val y : 'b
      method fst : 'a
      method get1 : 'a -> 'b
      method get2 : 'b -> 'a
      method print : unit -> unit
      method snd : 'b
    end
The method fst has type #printable where .. is unbound

This first attempt fails because methods fst and snd contain an open type.

So we shall keep the type parameters of the class, while constraining them to the open type #printable.


# class ['a,'b] printable_pair (x0 ) (y0 ) = 
   object
     constraint 'a = #printable
     constraint 'b = #printable 
     inherit ['a,'b] acc_pair x0 y0
     method print () = x#print(); y#print ()
   end;;
class ['a, 'b] printable_pair :
  'a ->
  'b ->
  object
    constraint 'a = #printable
    constraint 'b = #printable
    val x : 'a
    val y : 'b
    method fst : 'a
    method get1 : 'a -> 'b
    method get2 : 'b -> 'a
    method print : unit -> unit
    method snd : 'b
  end

Then we construct a displayable pair containing a point and a colored point.


# let pp = new printable_pair 
            (new point (1,2)) (new colored_point (3,4) "green");;
val pp : (point, colored_point) printable_pair = <obj>
# pp#print();;
( 1, 2)( 3, 4) with color green- : unit = ()

Parameterized Classes and Typing

From the point of view of types, a parameterized class is a parameterized type. A value of such a type can contain weak type variables.


# let r = new pair [] [];;
val r : ('_a list, '_b list) pair = <obj>
# r#fst;;
- : '_a list = []
# r#fst = [1;2];;
- : bool = false
# r;;
- : (int list, '_a list) pair = <obj>

A parameterized class can also be viewed as a closed object type; therefore nothing prevents us from also using it as an open type with the sharp notation.


# let compare_nothing ( x : ('a, 'a) #pair) = 
   if x#fst = x#fst then x#mess else x#mess2;;
val compare_nothing :
  < fst : 'a; mess : 'b; mess2 : 'b; snd : 'a; .. > -> 'b = <fun>

This lets us construct parameterized types that contain weak type variables that are also open object types.


# let prettytype x ( y : ('a, 'a) #pair) = if x = y#fst then y else y;;
val prettytype : 'a -> (('a, 'a) #pair as 'b) -> 'b = <fun>

If this function is applied to one parameter, we get a closure, whose type variables are weak. An open type, such as #pair, still contains uninstantiated parts, represented by the double point (..). In this respect, an open type is a partially known type parameter. Upon weakening such a type after a partial application, the displayer specifies that the type variable representing this open type has been weakened. Then the notation is _#pair.


# let g = prettytype 3;;
val g : ((int, int) _#pair as 'a) -> 'a = <fun>

Now, if function g is applied to a pair, its weak type is modified.


# g (new acc_pair 2 3);;
- : (int, int) acc_pair = <obj>
# g;;
- : (int, int) acc_pair -> (int, int) acc_pair = <fun>

Then we can no longer use g on simple pairs.


# g (new pair 1 1);;
Characters 4-16:
This expression has type (int, int) pair = < fst : int; snd : int >
but is here used with type
  (int, int) acc_pair =
    < fst : int; get1 : int -> int; get2 : int -> int; snd : int >
Only the second object type has a method get1

Finally, since parameters of the parameterized class can also get weakened, we obtain the following example.


# let h = prettytype [];;
val h : (('_b list, '_b list) _#pair as 'a) -> 'a = <fun>
# let h2 = h (new pair [] [1;2]);;
val h2 : (int list, int list) pair = <obj>
# h;;
- : (int list, int list) pair -> (int list, int list) pair = <fun>

The type of the parameter of h is no longer open. The following application cannot be typed because the argument is not of type pair.


# h (new acc_pair [] [4;5]);;
Characters 4-25:
This expression has type
  ('a list, int list) acc_pair =
    < fst : 'a list; get1 : 'a list -> int list; get2 : int list -> 'a list;
      snd : int list >
but is here used with type
  (int list, int list) pair = < fst : int list; snd : int list >
Only the first object type has a method get1

Note

Parameterized classes of Objective CAML are absolutely necessary as soon as one has methods whose type includes a type variable different from the type of self.