The RSA System

The RSA System is a public-key system named after its inventors, Rivest, Shamir, and Adleman (Rivest, R. L., Shamir, A., and Adleman, L., “A Method for Obtaining Digital Signatures and Public-Key Cryptosystems,” Comm. ACM, Vol. 21(2), Feb. 1978, pp. 120–128). Encryption and decryption are both performed by raising a large message block to an exponent in modular arithmetic. A public key consists of a modulus, which is the product of two large secret primes and an exponent. The corresponding private key consists of the modulus, the primes, and a secret exponent that cannot be determined without knowing the primes. The exponents are related in such a way that applying them in succession restores the original message.

Exhibit 8 illustrates this process. Each user in this exhibit has a public-private key pair based on a unique 512 to 1024 bit modulus n, where n = pq for secret primes p and q. The public key consists of n and an exponent e; the private key consists of n and a secret exponent d that is the inverse of e mod (p -1)(q -1). The secret primes p and q are also considered to be part of the private key, but once the exponents are generated, they are not used. For encryption, only the receiver’s keys are used. The sender encrypts a message block M by raising it to the receiver’s public exponent e (mod n). The receiver decrypts the ciphertext by raising it to its private exponent d (mod n). Decryption restores the original message because the relationship between e and d has the property that (M^e mod n)^d (modn) = (M^ed mod n) = M.

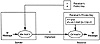
Exhibit 8.  An RSA Public-Key Cryptosystem

The key size is on the order of 512 to 1024 bits. This is about an order of magnitude greater than what is needed to protect against an attack by exhaustive search. The extra length is needed to protect against an attack based on factoring the modulus into its primes. For large numbers of 700 bits or more, factoring is thought to be intractable.

The RSA cryptosystem is considerably more time consuming than single-key systems, which typically use simple permutations and substitutions of bits. For this reason, it is not used to encrypt general communications or data. However, it is used to distribute the session key used with a single-key system. To send an encrypted message, the sender generates a session key, encrypts the message under the session key by using the single-key system, and encrypts the session key under the receiver’s public key by using RSA. The RSA-encrypted session key is then transmitted along with the encrypted message. Internet Privacy Enhanced Mail uses RSA and DES in this way to encrypt E-mail messages. It also uses RSA to compute digital signatures for messages.

Fair Public-Key Cryptosystems

A fair public-key cryptosystem has an objective similar to that of the escrowed encryption devices, namely to provide strong encryption for privacy and security while at the same time allowing law enforcement access when legally authorized. The concept, introduced by Silvio Micali (in “Fair Public-Key Cryptosystems,” Laboratory for Computer Science, MIT, Aug. 21, 1992), is realized by splitting each private key into multiple parts and registering each part with a separate key escrow agency. It differs from the escrowed encryption system in that the key parts are generated and distributed in such a way that a key management center can verify in advance that the distributed parts, when combined, will produce the original key. This is done using only the public key and other public information derived from the key parts. Another difference is that the escrowed keys are associated with a particular person rather than a device serial number.

The main advantage of Micali’s method is that it can be used with software encryption because it does not need any secret algorithms. In addition, it permits keys to be escrowed multiple times, for example, with the escrow agents of different countries and with the escrow agents chosen by a business. The main disadvantage is that it relies on a completely voluntary registration system; the key escrow process is not coupled with a manufacturing process. This drawback can be mitigated somewhat if registration of secret keys is coupled with the process of registering public keys for the purpose of obtaining a certificate establishing the authenticity of the key and its legal use for digital signatures and if software or hardware systems are written to require signed certificates. Another disadvantage is that the data base of keys associates the keys with particular persons.