DIGITAL SIGNATURE SYSTEMS

A digital signature is a block of data attached to a message (e.g., document, file, or record) that binds the message to a particular individual (or entity) such that the signature can be verified by the receiver or independent third party (e.g., a judge) and such that it cannot be forged. The binding is accomplished through a digital signature system, which is like a public-key cryptosystem in that each user has a public-private key pair that is used with a pair of functions. To sign a message, the sender first computes a condensed digest of the message using a public hash function. A cryptographic signature function, keyed to the sender’s private key, is then applied to the digest and the resulting digital signature is transmitted to the receiver along with the message. The receiver verifies the message by first hashing it to the digest and then applying a verification function, keyed to the sender’s public key, to the digest and signature. The message itself may be passed in the clear or in encrypted form by using some other method (see Exhibit 9).

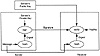
Exhibit 9.  A Public-Key Signature System

The hash function must have the property that for a given digest, it is practically impossible for the receiver or anyone else to find a second message with the same digest. This condition protects against the substitution of a bogus message at a later date. In addition, the function must have the property that it is practically impossible to find two different messages that hash to a common digest. This protects against someone generating two messages, only one of which the signer is willing to sign, and then later claiming that the other message was signed. The secure hash algorithm (SHA), which condenses a message to 160 bits, meets both conditions and has been adopted as the government standard.

Digital signatures provide nonrepudiation in that the signer cannot falsely deny having originated the message. Thus, digital signatures can be used with electronic contracts, purchase orders, and other legally binding documents in the same way that written signatures are used to sign such documents. In addition, digital signatures can be used to authenticate software (e.g., to protect against computer viruses), data, images, users, and machines. For example, a smart card with a digital signature capability can be used to authenticate a user to a computer.

The RSA public-key system can be used as a signature system as well as a cryptosystem. For signatures, the sender’s modulus and public and private exponents are used rather than the receiver’s, as is the case with encryption.

Exhibit 10 illustrates how an RSA signature system works. To send a signed message, the sender’s public-private key pair with modulus n and exponents e and d is used. To sign a message, the sender first hashes the message into a digest z using any hash method (e.g., MD5). The digest is then signed by raising it to the sender’s private exponent d (mod n). The resulting signature is transmitted to the receiver along with the original message, possibly encrypted if secrecy is also desired. After hashing the message (decrypting it first if necessary), the receiver validates the signature by raising it to the public exponent e (mod n) and verifying that the result is the same as the computed digest.

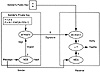
Exhibit 10.  RSA Signature System

The Digital Signature Standard

In 1991, NIST proposed a Digital Signature Standard (DSS) for government systems (“A Proposed Federal Information Processing Standard for Digital Signature Standard (DSS),” Federal Register, Vol. 56, Aug. 1991, p. 169). Unlike RSA, the DSS is strictly a signature system; it cannot be used as a cryptosystem for message secrecy. Because neither the signing function nor the verification function undoes the other, one cannot be used for encryption and the other for decryption (with RSA, both functions are identical and undo each other). The DSS uses the SHA to condense a message before signing (see Exhibit 11).

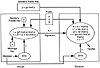
Exhibit 11.  The DSS

The DSS performs exponentiations of large numbers in modular arithmetic. The key size is 512 to 1024 bits, and security depends on the difficulty of inverting the exponentiations, that is, computing discrete logs. This is approximately the same as factoring; therefore, the security of DSS is comparable to that of RSA.

Public-Key Certificates

Public-key cryptosystems and signature systems are attractive because they can achieve secrecy by exchanging only public information. There is, however, a security risk with public keys, namely the substitution of fake public keys. For example, if a masquerader substitutes his or her own public key for that of some other person, others may accept signatures created by the masquerader, believing them to be from the masquerader’s victim.

To protect against this threat, public keys can be packaged in signed certificates that validate the keys. Before using a public key, the certificate is validated (i.e., its signature is checked). A certificate typically contains the user’s identification, public key, and a time or date stamp. It is digitally signed by a certification authority, whose own keys may be certified by a higher level authority up to some top-level authority. Certificates are obtained from the certification authority electronically. Once obtained, they can be cached or distributed with the messages that use their keys. NIST has sponsored a study of alternatives for automating management of public keys and certificates in both a national and an international environment.

SUMMARY

What does the future hold for escrowed encryption chips? Public-key methods for negotiating session keys and signing messages will be combined with the functions of the escrowed encryption chips to provide a general-purpose chip capable of implementing secure encryption, law enforcement access, and digital signatures. The enhanced chips, originally called Capstone, will include:

•  The SKIPJACK encryption algorithm.

•  The 80-bit KF.

•  A chip UID.

•  An 80-bit chip KU.

•  Specialized control software.

•  A public-key negotiation algorithm (probably Diffie-Hellman).

•  The DSA used with the DSS.

•  The SHA, also used with the DSS.

•  A general-purpose high-speed exponentiation algorithm.

•  A random number generator that uses a pure noise source.

The enhanced chips will initially be used by the Preliminary Message Security Protocol in the Defense Messaging System.