Definition. The impulse signal is denoted
In addition to difference-equation coefficients, any LTI filter may be represented in the time domain by its response to a specific signal called the impulse. This response is called, naturally enough, the impulse response of the filter. Any LTI filter can be implemented by convolving the input signal with the filter impulse response, as we will see.
Definition. The impulse signal is denotedand defined by
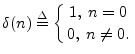
A plot of ![]() is given in Fig.5.2a. In the physical
world, an impulse may be approximated by a swift hammer blow (in the
mechanical case) or balloon pop (acoustic case). We also have a
special notation for the impulse response of a filter:
is given in Fig.5.2a. In the physical
world, an impulse may be approximated by a swift hammer blow (in the
mechanical case) or balloon pop (acoustic case). We also have a
special notation for the impulse response of a filter:
Definition. The impulse response of a filter is the response of the filter toand is most often denoted
:
We normally require that the impulse response decay to zero over time; otherwise, we say the filter is unstable. The next section formalizes this notion as a definition.