- ... analysis.2.1
- Testing a filter by
sweeping an input sinusoid through a range of frequencies is often
used in practice, especially when there might be some distortion that
also needs to be measured. There are particular advantages to using
exponentially swept sine-wave analysis [25], in which
the sinusoidal frequency increases exponentially with respect to time.
(The technique is sometimes also referred to as log-swept
sine-wave analysis.) Swept-sine analysis can be viewed as a
descendant of time-delay spectrometry.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...real2.2
- We may define a real filter as one whose
output signal is real whenever its input signal is real.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sinusoid|textbf.2.3
- Some authors refer to
 as a
complex exponential, but it is useful to reserve that term for
signals of the form
as a
complex exponential, but it is useful to reserve that term for
signals of the form
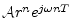 , where
, where 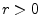 . That is,
complex exponentials are more generally allowed to have a
non-constant exponential amplitude envelope.
Note that all complex exponentials can be generated from two complex
numbers,
. That is,
complex exponentials are more generally allowed to have a
non-constant exponential amplitude envelope.
Note that all complex exponentials can be generated from two complex
numbers,
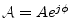 and
and
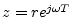 , viz.,
, viz.,
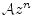 . This topic is explored further in [83].
. This topic is explored further in [83].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Octave,3.1
- Users of Matlab will also need the Signal Processing
Tool Box, which is available for an additional charge. Users of
Octave will also need the free ``Octave Forge'' collection, which
contains functions corresponding to the Signal Processing Tool Box.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
language.3.2
- In an effort to improve the matlab language, Octave
does not maintain 100% compatibility with Matlab. See
http://octave.sf.net/compatibility.html
for details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
form.''3.3
- As discussed in §5.3, a filter is said to
be ``causal'' if its current output does not depend on future inputs.
Direct-form filter implementations are discussed in Chapter 9.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...filter3.4
- Say help filter in Matlab or Octave
to view the documentation. In Matlab, you can also say doc
filter to view more detailed documentation in a Web browser.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
1.3.5
- As we will learn in §5.1, A(1) is the
coefficient of the current output sample, which is always
normalized to 1. The actual feedback coefficients are
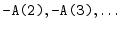 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... execution.3.6
- As a fine point, the fastest known FFT for
power-of-2 lengths is the split-radix FFT--a hybrid of the
radix-2 and radix-4 cases. See
http://cnx.org/content/m12031/latest/
for more details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT.3.7
- http://ccrma.stanford.edu/~jos/mdft/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
matlab4.1
- The term ``matlab'' (uncapitalized) will refer here to
either Matlab or Octave [82]. Code described
as ``matlab'' should run in either environment without modification.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... completeness.4.2
- Most plots in
this book are optimized for Matlab. Octave uses
gnuplot which is quite different from Matlab's
handle-oriented graphics. In Octave, the plots will typically be
visible, but the titles and axis labels are often incorrect due to the
different semantics associated with statement ordering in the two
cases.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frequency:4.3
- As always,
radian frequency
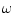 is related to frequency
is related to frequency  in Hz by the
relation
in Hz by the
relation
 . Also as always in this book, the sampling
rate is denoted by
. Also as always in this book, the sampling
rate is denoted by 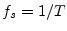 . Since the frequency axis for digital
signals goes from
. Since the frequency axis for digital
signals goes from  to
to 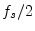 (non-inclusive), we have
(non-inclusive), we have
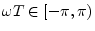 , where
, where 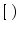 denotes a half-open interval. Since the
frequency
denotes a half-open interval. Since the
frequency
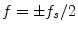 is usually rejected in applications, it is more
practical to take
is usually rejected in applications, it is more
practical to take
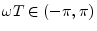 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
``echo''.4.4
- The minimum perceivable delay in audio work depends
very much on how the filter is being used and also on what signals are
being filtered. A few milliseconds of delay is usually not
perceivable in the monaural case. Note, however, that delay
perception is a function of frequency. One rule of thumb is that, to
be perceived as instantaneous, a filter's delay should be kept below a
few cycles at each frequency. A near-worst-case test signal for
monaural filter-delay perception is an impulse (pure click). (A
worst-case test would require some weighting vs. frequency.) Delay
distortion is less noticeable if all frequencies in a signal are
delayed by the same amount of time, since that preserves the original
waveshape exactly and delays it as a whole. Otherwise transient
smearing occurs, and the ear is fairly sensitive to onset synchrony
across different frequency bands.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...5.1
- In principle,
nonlinear filters can be considered a special case of time varying
filters, since any variation in the filter coefficients must occur
over time, and in the nonlinear case, this variation occurs in a
manner that depends on the input signal sample values. However, since
a constant signal (dc) does not vary over time, a nonlinear filter may
also be time-invariant. The key test for nonlinearity is whether the
filter coefficients change as a function of the input signal. A
linear time-varying filter, on the other hand,
must exhibit the same coefficient variation over time for
all input signals.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... outputs.5.2
- ``When you think about it, everything is a
filter.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... space5.3
- A set of vectors
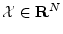 (or
(or 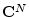 )
is said to form a vector space if
)
is said to form a vector space if
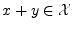 and
and
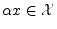 for all
for all
 ,
,
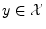 , and for all scalars
, and for all scalars
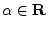 (or
(or 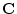 ) [70].
) [70].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... purposes.5.4
-
For more about the mathematics of linear vector spaces, look into
linear algebra [58] (which covers finite-dimensional
linear vector spaces) and/or operator theory
[56] (which treats the infinite-dimensional case).
The mathematical treatments used in this book will be closer to
complex analysis [14,43], but with some linear
algebra concepts popping up from time to time, especially in the
context of matlab examples. (The name ``matlab'' derives from ``matrix
laboratory,'' and it was originally written by Cleve Moler to be an
interactive desk-calculator front end for a library of numerical
linear algebra subroutines (LINPACK and EISPACK).
As a result, matlab syntax is designed to follow linear algebra
notation as closely as possible.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... domain.6.1
- The term ``difference
equation'' is a discrete-time counterpart to the term ``differential
equation'' in continuous time. LTI difference equations in discrete
time correspond to linear differential equations with
constant coefficients in continuous time. The subject of
finite differences is devoted to ``discretizing'' differential
equations to obtain difference equations [96,3].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
scheme|textbf.6.2
- The term ``explicit'' in this context means that the
output
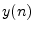 at time
at time 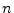 can be computed using only past
output samples
can be computed using only past
output samples 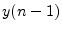 ,
, 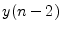 , etc. When solving partial
differential equations numerically on a grid in 2 or more dimensions,
it is possible to derive finite difference schemes which cannot be
computed recursively, and these are termed implicit finite
difference schemes [96,3]. Implicit schemes can
often be converted to explicit schemes by a change of coordinates
(e.g., to modal coordinates [85]).
, etc. When solving partial
differential equations numerically on a grid in 2 or more dimensions,
it is possible to derive finite difference schemes which cannot be
computed recursively, and these are termed implicit finite
difference schemes [96,3]. Implicit schemes can
often be converted to explicit schemes by a change of coordinates
(e.g., to modal coordinates [85]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... filter.6.3
- Instead of defining
the impulse response as the response of the filter to
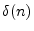 , a
unit-amplitude impulse arriving at time zero, we could equally well
choose our ``standard impulse'' to be
, a
unit-amplitude impulse arriving at time zero, we could equally well
choose our ``standard impulse'' to be
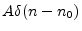 , an
amplitude-
, an
amplitude-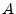 impulse arriving at time
impulse arriving at time 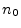 . However, setting
. However, setting
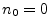 and
and 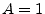 makes the math simpler to write, as we will see.
makes the math simpler to write, as we will see.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT6.4
- http://ccrma.stanford.edu/~jos/mdft/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT6.5
- http://ccrma.stanford.edu/~jos/mdft/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sinusoid).6.6
- We can also use the term ``stationary'' in
place of ``steady state'' for signals that are a fixed linear
combination of a finite number of sinusoids. However, in signal
processing, the term ``stationary signal'' normally means ``stationary
noise signal'', or, more precisely, ``stationary stochastic process''.
In either case, we are simply talking about the decomposition of
signals into transient and steady-state components, or transient and
stationary components.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
filters.6.7
- A short tutorial on matrices appears
in [83], available online at
http://ccrma.stanford.edu/~jos/mdft/Matrices.html.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT.6.8
- http://ccrma.stanford.edu/~jos/mdft/Matrix_Formulation_DFT.html.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT6.9
- http://ccrma.stanford.edu/~jos/mdft/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... properties.6.10
- http://en.wikipedia.org/wiki/Circulant_matrix
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... follows:6.11
- While this
example is easily done by hand, the matlab function tf2ss
can be used more generally (``transfer function to state space''
conversion).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
way.6.12
- The methods discussed in this section are intended for
LTI system identification. Many valued guitar-amplifier modes, of
course, provide highly nonlinear distortion. Identification of
nonlinear systems is a relatively advanced topic with lots of special
techniques
[25,17,97,4,86].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
derive.6.13
- There are many possible definitions of pseudoinverse
for a matrix
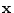 . The Moore-Penrose pseudoinverse is perhaps most
natural because it gives the least-squares solution to the set
of simultaneous linear equations
. The Moore-Penrose pseudoinverse is perhaps most
natural because it gives the least-squares solution to the set
of simultaneous linear equations
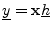 , as we show later in
this section.
, as we show later in
this section.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Golub.6.14
- Say help slash in Matlab.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...7.1
- Remember that the
transfer function of a filter is defined by
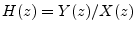 , where
, where
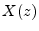 is the input-signal z transform, and
is the input-signal z transform, and 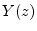 is the output-signal z transform.
If we have two filters
is the output-signal z transform.
If we have two filters
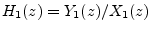 and
and
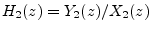 , and we arrange them in series such that filter
1 is applied first, followed by filter 2, then we have
, and we arrange them in series such that filter
1 is applied first, followed by filter 2, then we have
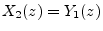 . Consequently, the overall transfer function becomes
. Consequently, the overall transfer function becomes
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... terms,7.2
- By the fundamental theorem of algebra, a
polynomial
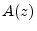 of any degree can be completely factored as a
product of one-zero polynomials, where the zeros may be complex.
of any degree can be completely factored as a
product of one-zero polynomials, where the zeros may be complex.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
coefficients.7.3
- At the time of this writing, there is no
residuez function for Octave, although it does have residue
for continuous-time-filter (
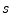 -plane transfer-function) partial
fraction expansions. In §H.5, an implementation of
residuez in termsof residue is provided.
-plane transfer-function) partial
fraction expansions. In §H.5, an implementation of
residuez in termsof residue is provided.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...biquads.7.4
- A biquad is simply a
second-order filter section--see §10.1.6 for details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
function|textbf.7.5
- The case
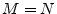 is called a proper transfer
function, and
is called a proper transfer
function, and 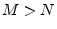 is termed improper.
is termed improper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
on:7.6
-
These closed-form sums were quickly computed using the
free symbolic mathematics program called maxima running under
Linux, specifically by typing
factor(ev(sum(m+1,m,0,n),simpsum)); followed by
factor(ev(sum(%,n,0,m),simpsum));.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...B2.7.7
- Since convolution is
commutative,
either operand to a convolution can be interpreted as the filter
impulse-response while the other is interpreted as the input
signal. However, in the matlab filter function, the operand
designated as the input signal (3rd argument) determines the length to
which the output signal is truncated.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...freqzdemo2.8.1
- The ``multiplot''
created by the plotfr utility (§H.4) cannot be
saved to disk in Octave, although it looks fine on screen. In Matlab,
there is no problem saving multiplots to disk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....8.2
- The quantity
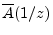 is known as the
para-Hermitian conjugate of the polynomial
is known as the
para-Hermitian conjugate of the polynomial 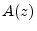 . It coincides
with the ordinary complex conjugate along the unit
circle, while elsewhere in the
. It coincides
with the ordinary complex conjugate along the unit
circle, while elsewhere in the 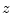 -plane,
-plane, 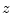 is replaced by
is replaced by 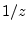 and
only the coefficients of
and
only the coefficients of 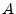 are conjugated. A mathematical feature
of the para-Hermitian conjugate is that
are conjugated. A mathematical feature
of the para-Hermitian conjugate is that
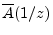 is an
analytic function of
is an
analytic function of 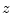 while
while
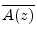 is not.
is not.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....9.1
- As mentioned
in §6.2 and discussed further in §B.1, the domain of the
z transform can be extended to the rest of the
complex plane by means of analytic continuation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... grow.9.2
- As discussed in §6.8.5, the
impulse response of a repeated pole of multiplicity
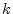 at a
point on the unit circle grows with amplitude envelope proportional to
at a
point on the unit circle grows with amplitude envelope proportional to
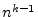 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...SmithPASP.9.3
-
http://ccrma.stanford.edu/~jos/pasp/Passive_Reflectances.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
time-constant|textbf9.4
- Decay time constants were introduced in Book I
[83] of this series (``Exponentials''). The time
constant
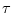 is formally defined for exponential decays as the
time it takes to decay by the factor
is formally defined for exponential decays as the
time it takes to decay by the factor 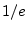 . In audio signal
processing, exponential decay times are normally defined instead as
. In audio signal
processing, exponential decay times are normally defined instead as
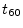 or
or 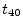 , etc., where
, etc., where 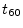 , e.g., is the time to decay
by 60 dB. A quick calculation reveals that
, e.g., is the time to decay
by 60 dB. A quick calculation reveals that 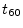 is a little less
than seven time constants (
is a little less
than seven time constants (
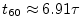 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....9.5
- The
residue of a pole
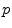 is simply the coefficient of
is simply the coefficient of
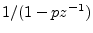 as
as 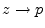 . See §6.8 for details.
. See §6.8 for details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT10.1
- http://ccrma.stanford.edu/~jos/mdft/Two_s_Complement_Fixed_Point_Format.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...GrayAndMarkel75,MG,SmithPASP.10.2
- http://ccrma.stanford.edu/~jos/pasp/Conventional_Ladder_Filters.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tf2sos|textbf10.3
- In
Matlab, the Signal Processing Tool Box is required for second-order
section support. In Octave, the free Octave-Forge add-on collection
is required.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Octave.10.4
- The Matlab Signal Processing Tool Box has even
more -- say ``lookfor sos'' in Matlab to find them all.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...10.5
- As mentioned in
§1.3.2, a real filter yields a real output signal for all real
input signals. In particular, a filter is real if and only if each
sample of its impulse response is real. IIR filters are real when
each coefficient is real.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
bandwidths10.6
- See §C.6 for a definition of half-power
bandwidth.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... series.10.7
- In this
particular case, there is an even better structure known as a
ladder filter that can be interpreted as a physical
model of the vocal tract [48,86].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...pfe).10.8
- In practice, it is not critical to get the
biquad numerators exactly right. In fact, the vowel still sounds ok
if all the biquad numerators are set to 1, in which case, nulls are
introduced between the formant resonances in the spectrum. The ear is
not nearly as sensitive to spectral nulls as it is to spectral peaks.
Furthermore, natural listening environments introduce nulls quite
often, such as when a direct signal is mixed with its own reflection
from a flat surface (such as a wall or floor).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... overflow.11.1
- A small chance of
overflow remains because sinusoids at different frequencies can be
delayed differently by the filter, causing an increased peak amplitude
in the output due to phase realignment.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...resonance11.2
- A
resonance may be defined as a local peak in the amplitude
response of a filter, caused by a pole close to the unit circle.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... case,11.3
- In the case of complex coefficients
 ,
,
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... applications.11.4
- For the reader with some background
in analog circuit design, the dc blocker is the digital equivalent of
the analog blocking capacitor.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... response,11.5
- See §8.1
in Chapter 8.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... virtual11.6
- The term
virtual analog synthesis refers to digital implementations
of classic analog synthesizers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...even.12.1
- In the complex case,
the zero-phase impulse response is Hermitian, i.e.,
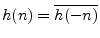 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... algorithm.12.2
- The remez function is
implemented in the Matlab signal processing tool box and in the Octave
Forge collection.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
filter.12.3
- They can also be derived as the
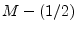 sample delay
of a length
sample delay
of a length 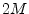 zero-phase filter, but this requires being able to
interpolate the zero-phase filter coefficients using ideal bandlimited
interpolation [91], which, in principle, results
in an IIR filter.
zero-phase filter, but this requires being able to
interpolate the zero-phase filter coefficients using ideal bandlimited
interpolation [91], which, in principle, results
in an IIR filter.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....13.1
- Another way to show that all minimum-phase filters and
their inverses are causal, using the Cauchy integral theorem from
complex variables
[14], is to consider a Laurent series expansion of the transfer
function
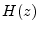 about any point on the unit circle. Because all poles
are inside the unit circle (for either
about any point on the unit circle. Because all poles
are inside the unit circle (for either 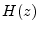 or
or 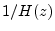 ), the
expansion is one-sided (no positive powers of
), the
expansion is one-sided (no positive powers of 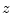 ). A Laurent
expansion about a point on the unit circle redefines unstable poles as
noncausal exponentials (which decay toward
). A Laurent
expansion about a point on the unit circle redefines unstable poles as
noncausal exponentials (which decay toward 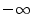 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... phase,13.2
- The convolution of two minimum phase
sequences is minimum phase, since this just doubles each pole and zero
in place, so they remain inside the unit circle.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...tmps.13.3
- A Mathematica notebook for this
purpose was written by Andrew Simper, available at
http://www.vellocet.com/dsp/MinimumPhase/MinimumPhase.html
http://www.vellocet.com/dsp/MinimumPhase/MinimumPhase.nb
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT.A.1
- http://ccrma.stanford.edu/ jos/mdft/Sinusoids_Exponentials.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MDFT.A.2
- http://ccrma.stanford.edu/~jos/mdft/Discrete_Fourier_Transform_DFT.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...causalB.1
- A signal
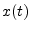 is said to be
causal if it is zero for all
is said to be
causal if it is zero for all 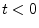 . A system is said to be causal if
its response to an input never occurs before the input is received;
thus, an LTI filter is a causal system whenever its impulse response
. A system is said to be causal if
its response to an input never occurs before the input is received;
thus, an LTI filter is a causal system whenever its impulse response
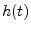 is a causal signal.
is a causal signal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
order,B.2
- The order of a pole is its multiplicity. For example,
the function
 has a pole at
has a pole at 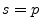 of order 3.
of order 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... there''.B.3
- Note that, mathematically,
our solution specifies that the mass position is zero prior to time
0. Since we are using the unilateral Laplace transform, there is
really ``no such thing'' as time less than zero, so this is
consistent. Using the
bilateral Laplace transform, the same solution is obtained if
the mass is at position
 for all negative time
for all negative time 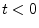 , and the
driving force
, and the
driving force 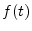 imparts a doublet having ``amplitude''
imparts a doublet having ``amplitude''
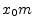 at time 0, i.e.,
at time 0, i.e.,
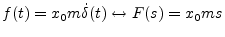 , and all initial conditions are taken to be zero (as they
must be for the bilateral Laplace transform). A
doublet is defined as the time-derivative of the impulse
signal (defined in Eq. (C.5)). In other words, impulsive inputs
at time 0 can be used to set up arbitrary initial
conditions. Specifically, the input
, and all initial conditions are taken to be zero (as they
must be for the bilateral Laplace transform). A
doublet is defined as the time-derivative of the impulse
signal (defined in Eq. (C.5)). In other words, impulsive inputs
at time 0 can be used to set up arbitrary initial
conditions. Specifically, the input
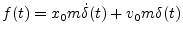 slams the system into initial state
slams the system into initial state 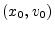 at
time 0.
at
time 0.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...causal|textbfD.1
- Recall that a filter is said to be
causal if its impulse response
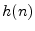 is zero for
is zero for 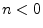 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... have,D.2
- Note that the
time-domain norm
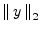 is unnormalized (which it must
be) while the frequency-domain norm
is unnormalized (which it must
be) while the frequency-domain norm
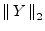 is normalized
by
is normalized
by
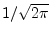 . This is the cleanest choice of
. This is the cleanest choice of 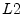 norm definitions
for present purposes.
norm definitions
for present purposes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... FiltersD.3
- This section is relatively advanced and can be omitted without loss of continuity in what follows.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... FiltersD.4
- This section is relatively advanced and can be omitted without loss of continuity in what follows.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrix,E.1
- A short tutorial on matrices appears
in [83], available online at
http://ccrma.stanford.edu/~jos/mdft/Matrices.html.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
elsewhere.E.2
- I.e.,
 , where
, where
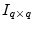 is the
is the  identity matrix, and
identity matrix, and 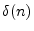 denotes the
discrete-time impulse signal (which is 1 at time
denotes the
discrete-time impulse signal (which is 1 at time 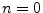 and zero for
all
and zero for
all 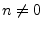 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrix.E.3
- To emphasize something is a matrix, it is often
typeset in a boldface font. In this appendix, however, capital
letters are more often used to denote matrices.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... series,E.4
- Let
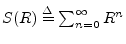 , where
, where 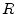 is a square matrix.
Then
is a square matrix.
Then
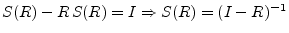 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....E.5
- Equivalently, a causal transfer function
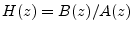 contains a delay-free path whenever
contains a delay-free path whenever
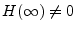 , since
, since
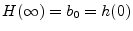 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
model.E.6
- An exception arises when the model may be time
varying. A time varying
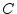 matrix, for example, will cause
time-varying zeros in the system. These zeros may momentarily cancel
poles, rendering them unobservable for a short time.
matrix, for example, will cause
time-varying zeros in the system. These zeros may momentarily cancel
poles, rendering them unobservable for a short time.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
quasi-harmonicE.7
- The overtones of a vibrating string are never
exactly harmonic because all strings have some finite
stiffness. This is why we call them ``overtones'' instead of
``harmonics.'' A perfectly flexible ideal string may have exactly
harmonic overtones [55].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form.E.8
- As
of this writing, this function does not exist in Octave or Octave
Forge, but it is easily simulated using sos2tf followed by
tf2ss.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
matlab.E.9
- Specifically, this example was computed using
Octave's tf2ss. Matlab gives a different but equivalent form
in which the state variables are ordered in reverse. The effect is a
permutation given by flipud(fliplr(M)), where
M denotes the matrix A, B, or C. In other
words, the two state-space models are obtained from each other using
the similarity transformation matrix
T=[0 0 1; 0 1 0; 1 0 0] (a simple permutation matrix).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... numerically.E.10
- If the Matlab
Control Tool Box is available, there are higher level routines for
manipulating state-space representations; type ``lookfor
state-space'' in Matlab to obtain a summary, or do a search on the
Mathworks website. Octave tends to provide its control-related
routines in the base distribution of Octave.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....E.11
- In general,
we can write an order
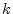 Jordan block
Jordan block  corresponding to eigenvalue
corresponding to eigenvalue
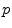 as
where
as
where 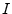 denotes the
denotes the 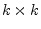 identity matrix, and
Note that
identity matrix, and
Note that 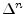 , for
, for
 has ones along the
has ones along the  th
superdiagonal and zeros elsewhere. Also,
th
superdiagonal and zeros elsewhere. Also,
 for
for  .
By the binomial theorem,
.
By the binomial theorem,
where
![$ \left(\begin{array}{c} n \\ [2pt] k \end{array}\right)\isdef n!/[k!(n-k)!]$](img2166.png) denotes the binomial coefficient (also
called ``
denotes the binomial coefficient (also
called ``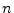 choose
choose 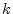 '' in probability theory).
Thus,
'' in probability theory).
Thus,
where the zeros in the upper-right corner are valid for
sufficiently large 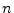 , and otherwise the indicated series
is simply truncated.
, and otherwise the indicated series
is simply truncated.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
matrix.F.1
- Recursive filters are brought into this framework in
the time-invariant case by dealing directly with their impulse
response, or the so called moving average representation.
Linear time-varying recursive filters have a matrix representation,
but it is not easy to find. In general one must symbolically
implement the equation
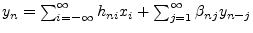 and collect coefficients of
and collect coefficients of  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dc).G.1
- In other
words, matching leading terms in the Taylor series expansion of
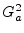 about
about
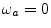 determines the poles as a function of the
zeros, leaving the zeros unconstrained. It is shown in
[63] that any filter of the form
is maximally flat at dc, where
determines the poles as a function of the
zeros, leaving the zeros unconstrained. It is shown in
[63] that any filter of the form
is maximally flat at dc, where
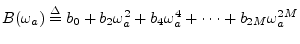 , with
, with  necessary
to force a zero at
necessary
to force a zero at
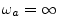 . Choosing maximum flatness also
at
. Choosing maximum flatness also
at
 pushes all the zeros out to infinity, giving the
simple form in Eq. (G.1). It is noted in [63]
how the more general class of Butterworth lowpass filters can be used
to provide maximum flatness at dc while obtaining more general
spectral shapes, such as notches at specific finite frequencies.
pushes all the zeros out to infinity, giving the
simple form in Eq. (G.1). It is noted in [63]
how the more general class of Butterworth lowpass filters can be used
to provide maximum flatness at dc while obtaining more general
spectral shapes, such as notches at specific finite frequencies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... causalG.2
-
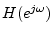 is said to be causal if
is said to be causal if
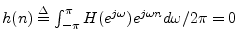 for
for 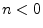 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Octave.H.1
- On a Red Hat Fedora
Core Linux system, octave-forge is presently in ``Fedora
Extras'', so that one can simply type yum install
octave-forge at a shell prompt (as root).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
complex):H.2
- Thanks to Matt Wright for contributing the original
version of this example.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...PASPI.1
- http://ccrma.stanford.edu/~jos/pasp/Getting_Started_Synthesis_Tool.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
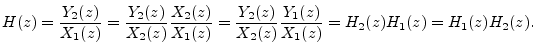
![$\displaystyle \Delta \isdef
\left[\begin{array}{ccccc}
0 & 1 & 0 & \cdots & 0...
...0 & 0 & 0 & \ddots & 1 \\ [2pt]
0 & 0 & 0 & \cdots & 0 \\
\end{array}\right].
$](img2160.png)

![$ \left(\begin{array}{c} n \\ [2pt] k \end{array}\right)\isdef n!/[k!(n-k)!]$](img2166.png) denotes the binomial coefficient (also
called ``
denotes the binomial coefficient (also
called ``![]() choose
choose ![]() '' in probability theory).
Thus,
'' in probability theory).
Thus,
![$\displaystyle J^n =
\left[\begin{array}{cccccccc}
p^n & np^{n-1} & \frac{n(n-...
... 0 & 0 & & & np^{n-1}\\ [2pt]
0 & 0 & 0 & & & p^n \\ [2pt]
\end{array}\right],
$](img2167.png)