To show by means of phasor analysis that Eq. (A.1) always has a solution, we can express each component sinusoid as
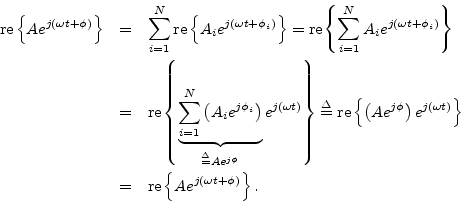
Thus, equality holds when we define
As is often the case, we see that the use of Euler's identity and complex analysis gives a simplified algebraic proof which replaces a proof based on trigonometric identities.