The magnitude ![]() of a complex pole determines the
damping or bandwidth of the resonator. (Damping may be
defined as the reciprocal of the bandwidth.)
of a complex pole determines the
damping or bandwidth of the resonator. (Damping may be
defined as the reciprocal of the bandwidth.)
When ![]() is close to 1, a reasonable definition of bandwidth
is close to 1, a reasonable definition of bandwidth ![]() is
provided by
is
provided by
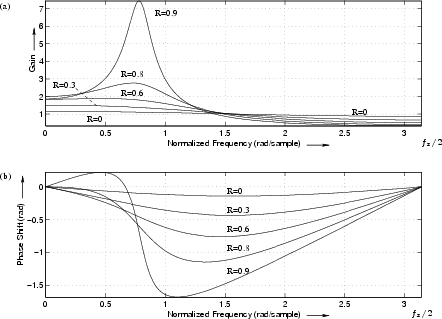
Figure 10.7 shows a family of frequency responses for the
two-pole resonator obtained by setting ![]() and varying
and varying ![]() . The
value of
. The
value of ![]() , in all cases is
, in all cases is ![]() , corresponding to
, corresponding to
![]() . The analytic expressions for amplitude and phase response are
. The analytic expressions for amplitude and phase response are
![\begin{eqnarray*}
G(\omega)\! &=&
\!\frac{b_0}{\sqrt{[1 + a_1 \cos(\omega T) + a...
... + a_1 \cos(\omega T) + a_2 \cos(2\omega T)}\right]\qquad(b_0>0)
\end{eqnarray*}](img1256.png)
where
![]() and
and ![]() .
.
 |