Discrete Time Fourier Transform (DTFT)

The Discrete Time Fourier Transform (DTFT) can be viewed as the limiting form of the DFT when its length $N$ is allowed to approach infinity:

$$X(\tilde{\omega}) \isdef \sum_{n=-\infty}^\infty x(n) e^{-j\tilde{\omega}n}$$

where $\tilde{\omega}\isdef \omega T\in[-\pi,\pi)$ denotes the continuous normalized radian frequency variable,^B.1 and $x(n)$ is the signal amplitude at sample number $n$.

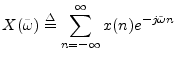
The inverse DTFT is

$$x(n) = \frac{1}{2\pi}\int_{-\pi}^\pi X(\tilde{\omega}) e^{j\tilde{\omega}n} d\tilde{\omega}$$

which can be derived in a manner analogous to the derivation of the inverse DFT (see Chapter 6).

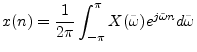
Instead of operating on sampled signals of length $N$ (like the DFT), the DTFT operates on sampled signals $x(n)$ defined over all integers $n\in{\bf Z}$. As a result, the DTFT frequencies form a continuum. That is, the DTFT is a function of continuous frequency $\tilde{\omega}\in[-\pi,\pi)$, while the DFT is a function of discrete frequency $\omega_k$, $k\in[0,N-1]$. The DFT frequencies $\omega_k=2\pi k/N$, $k=0,1,2,\ldots,N-1$, are given by the angles of $N$ points uniformly distributed along the unit circle in the complex plane (see Fig.6.1). Thus, as $N\to\infty$, a continuous frequency axis must result in the limit along the unit circle in the $z$ plane. The axis is still finite in length, however, because the time domain remains sampled.