The DFT is defined only for frequencies
![]() . If we
are analyzing one or more periods of an exactly periodic signal, where the
period is exactly
. If we
are analyzing one or more periods of an exactly periodic signal, where the
period is exactly ![]() samples (or some integer divisor of
samples (or some integer divisor of ![]() ), then these
really are the only frequencies present in the signal, and the spectrum is
actually zero everywhere but at
), then these
really are the only frequencies present in the signal, and the spectrum is
actually zero everywhere but at
![]() ,
,
![]() .
However, we use the
DFT to analyze arbitrary signals from nature. What happens when a
frequency
.
However, we use the
DFT to analyze arbitrary signals from nature. What happens when a
frequency ![]() is present in a signal
is present in a signal ![]() that is not one of the
DFT-sinusoid frequencies
that is not one of the
DFT-sinusoid frequencies ![]() ?
?
To find out, let's project a length ![]() segment of a sinusoid at an
arbitrary frequency
segment of a sinusoid at an
arbitrary frequency ![]() onto the
onto the ![]() th DFT sinusoid:
th DFT sinusoid:
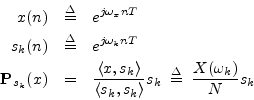
The coefficient of projection is proportional to
![\begin{eqnarray*}
X(\omega_k) & \isdef & \left<x,s_k\right> \;\isdef \; \sum_{n=...
...ac{\sin[(\omega_x-\omega_k)NT/2]}{\sin[(\omega_x-\omega_k)T/2]},
\end{eqnarray*}](img1044.png)
using the closed-form expression for a geometric series sum once
again. As shown in §6.3-§6.4 above,
the sum is ![]() if
if
![]() and zero at
and zero at ![]() , for
, for ![]() . However,
the sum is nonzero at all other frequencies
. However,
the sum is nonzero at all other frequencies ![]() .
.
Since we are only looking at ![]() samples, any sinusoidal segment can be
projected onto the
samples, any sinusoidal segment can be
projected onto the ![]() DFT sinusoids and be reconstructed exactly by a
linear combination of them. Another way to say this is that the DFT
sinusoids form a basis for
DFT sinusoids and be reconstructed exactly by a
linear combination of them. Another way to say this is that the DFT
sinusoids form a basis for ![]() , so that any length
, so that any length ![]() signal
whatsoever can be expressed as linear combination of them. Therefore, when
analyzing segments of recorded signals, we must interpret what we see
accordingly.
signal
whatsoever can be expressed as linear combination of them. Therefore, when
analyzing segments of recorded signals, we must interpret what we see
accordingly.
The typical way to think about this in practice is to consider the DFT
operation as a digital filter for each ![]() , whose input is
, whose input is ![]() and whose output is
and whose output is
![]() at time
at time ![]() .6.4 The
frequency response of this filter is what we just
computed,6.5 and its magnitude is
.6.4 The
frequency response of this filter is what we just
computed,6.5 and its magnitude is
![$\displaystyle \left\vert X(\omega_k)\right\vert =
\left\vert\frac{\sin[(\omega_x-\omega_k)NT/2]}{\sin[(\omega_x-\omega_k)T/2]}\right\vert
$](img1050.png)
![\includegraphics[width=\textwidth]{eps/dftfilter}](img1055.png) |
We see that
![]() is sensitive to all frequencies between dc
and the sampling rate except the other DFT-sinusoid frequencies
is sensitive to all frequencies between dc
and the sampling rate except the other DFT-sinusoid frequencies
![]() for
for ![]() . This is sometimes called spectral leakage
or cross-talk in the spectrum analysis. Again, there is no
leakage when the signal being analyzed is truly periodic and we can choose
. This is sometimes called spectral leakage
or cross-talk in the spectrum analysis. Again, there is no
leakage when the signal being analyzed is truly periodic and we can choose
![]() to be exactly a period, or some multiple of a period. Normally,
however, this cannot be easily arranged, and spectral leakage can
be a problem.
to be exactly a period, or some multiple of a period. Normally,
however, this cannot be easily arranged, and spectral leakage can
be a problem.
Note that peak spectral leakage is not reduced by increasing
![]() .6.7 It can be thought of as being caused by abruptly
truncating a sinusoid at the beginning and/or end of the
.6.7 It can be thought of as being caused by abruptly
truncating a sinusoid at the beginning and/or end of the
![]() -sample time window. Only the DFT sinusoids are not cut off at the
window boundaries. All other frequencies will suffer some truncation
distortion, and the spectral content of the abrupt cut-off or turn-on
transient can be viewed as the source of the sidelobes. Remember
that, as far as the DFT is concerned, the input signal
-sample time window. Only the DFT sinusoids are not cut off at the
window boundaries. All other frequencies will suffer some truncation
distortion, and the spectral content of the abrupt cut-off or turn-on
transient can be viewed as the source of the sidelobes. Remember
that, as far as the DFT is concerned, the input signal ![]() is the
same as its
periodic extension (more about this in
§7.1.2). If we repeat
is the
same as its
periodic extension (more about this in
§7.1.2). If we repeat ![]() samples of a sinusoid at frequency
samples of a sinusoid at frequency
![]() (for any
(for any
![]() ), there will be a ``glitch''
every
), there will be a ``glitch''
every ![]() samples since the signal is not periodic in
samples since the signal is not periodic in ![]() samples.
This glitch can be considered a source of new energy over the entire
spectrum. See
Fig.8.3 for an example waveform.
samples.
This glitch can be considered a source of new energy over the entire
spectrum. See
Fig.8.3 for an example waveform.
To reduce spectral leakage (cross-talk from far-away
frequencies), we typically use a
window
function, such as a
``raised cosine'' window, to taper the data record gracefully
to zero at both endpoints of the window. As a result of the smooth
tapering, the main lobe widens and the sidelobes
decrease in the DFT response. Using no window is better viewed as
using a rectangular window of length ![]() , unless the signal is
exactly periodic in
, unless the signal is
exactly periodic in ![]() samples. These topics are considered further
in Chapter 8.
samples. These topics are considered further
in Chapter 8.