The inner product (or ``dot product'', or ``scalar product'')
is an operation on two vectors which produces a scalar. Defining an
inner product for a Banach space specializes it to a Hilbert
space (or ``inner product space''). There are many examples of
Hilbert spaces, but we will only need
![]() for this
book (complex length
for this
book (complex length ![]() vectors, and complex scalars).
vectors, and complex scalars).
The inner product between (complex) ![]() -vectors
-vectors
![]() and
and
![]() is
defined by5.9
is
defined by5.9
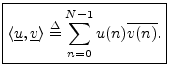
The complex conjugation of the second vector is done in order that a norm will be induced by the inner product:5.10

Note that the inner product takes
![]() to
to ![]() . That
is, two length
. That
is, two length ![]() complex vectors are mapped to a complex scalar.
complex vectors are mapped to a complex scalar.