Linearity of the Inner Product
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Any function
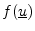 of a vector
of a vector
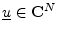 (which we may call an
operator on
(which we may call an
operator on 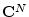 ) is said to be linear if for all
) is said to be linear if for all
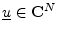 and
and
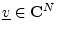 , and for all scalars
, and for all scalars 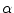 and
and 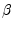 in
in
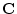 ,
,
A linear operator thus ``commutes with mixing.''
Linearity consists of two component properties:
- additivity:
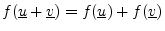
- homogeneity:
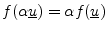
A function of multiple vectors, e.g.,
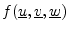 can be linear or not
with respect to each of its arguments.
can be linear or not
with respect to each of its arguments.
The inner product
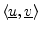 is linear in its first argument, i.e.,
for all
is linear in its first argument, i.e.,
for all
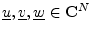 , and for all
, and for all
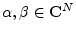 ,
,
This is easy to show from the definition:
The inner product is also additive in its second argument, i.e.,
but it is only conjugate homogeneous (or antilinear)
in its second argument, since
The inner product is strictly linear in its second argument with
respect to real scalars 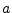 and
and 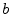 :
:
where
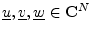 .
.
Since the inner product is linear in both of its arguments for real
scalars, it may be called a bilinear operator in that
context.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy]
![]() of a vector
of a vector
![]() (which we may call an
operator on
(which we may call an
operator on ![]() ) is said to be linear if for all
) is said to be linear if for all
![]() and
and
![]() , and for all scalars
, and for all scalars ![]() and
and ![]() in
in
![]() ,
,
![]() is linear in its first argument, i.e.,
for all
is linear in its first argument, i.e.,
for all
![]() , and for all
, and for all
![]() ,
,
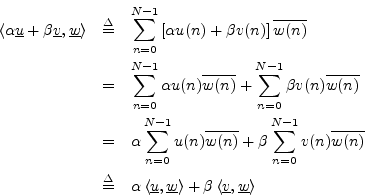
![]() and
and ![]() :
: