More Notation and Terminology

It's already been mentioned that the rectilinear coordinates of a complex number $z = x + jy$ in the complex plane are called the real part and imaginary part, respectively.

We also have special notation and various names for the polar coordinates $(r,\theta)$ of a complex number $z$:

$$\begin{eqnarray*} r &\isdef & \left\vert z\right\vert = \sqrt{x^2 + y^2}\\ &=&... ...!argument, angle, or phase\vert textbf}, or \emph{phase} of $z$} \end{eqnarray*}$$

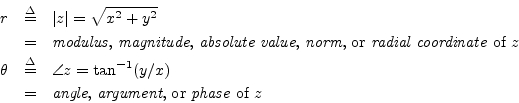
The complex conjugate of $z$ is denoted $\overline{z}$ (or $z^\ast$) and is defined by

$$\zbox {\overline{z} \isdef x - j y}$$

where, of course, $z\isdef x+jy$.

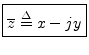
In general, you can always obtain the complex conjugate of any expression by simply replacing $j$ with $-j$. In the complex plane, this is a vertical flip about the real axis; i.e., complex conjugation replaces each point in the complex plane by its mirror image on the other side of the $x$ axis.