4.9.2 Important Optimization Result
A question that naturally arises in the design
of queueing systems with priorities is how these priorities should be assigned to
accomplish some desirable objective with regard to the performance of the queueing system.
Obviously, the answer to this question will depend on the characteristics of the queueing
system at hand and on the nature of the desirable objective. In general, questions of this
type are among the most difficult to deal with in queueing theory.
A most useful result in this area has been
obtained for the nonpreemptive M/G/1 priority system which we have just analyzed. We
consider again r distinct classes of users with Poisson arrivals (at a rate 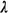 k,
for class k) and general service times (with mean 1/ k, for class k) and with
the priority arrangement described through Figure 4.15. Let us assume that for each class
of users there is a cost ck, (k = 1, 2, . . . ,
r) for each unit of time that a user from this class spends in the system (in queue or in
service).
Suppose, then, that the objective is to
minimize the average cost to all users per unit of time (for steady-state conditions);
that is, we wish to minimize
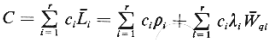(4.109)
Then the following holds true:
Theorem: To minimize (4.109) compute for each class k,
the ratio fk, = Ck/(1/k).
Then assign priorities according to the relative magnitudes of the r ratios: specifically,
the higher the value of the ratio, the higher the priority of the class.
In other words, we reorder the subscripts
of the ratios fk, so that
Then the class of users that corresponds to the ratio f1
(i.e., that incurs the highest cost per unit of service time) is assigned top priority for
access to the server, the class corresponding to the ratio f2
second highest priority, and so on. Note that this result holds only for the case when the
costs of system time (or of waiting time) increase linearly with system (or waiting) time
for all classes of users.
No formal proof of the theorem will be
presented here (the reader may wish to consult [KLEI 76], for one). It is simple, however,
to argue intuitively for the theorem's validity by recognizing that minimizing C in
(4.109) is the same as minimizing the expected area between the "cost
inflow" and "cost outflow" curves in Figure 4.16. This figure is a modified
version of Figure 4.3 in which the vertical axis represents "cost" instead of
"number of users." We have no control over the "cost inflow" curve
whose expected rate of growth per unit of time is constant and equal to  .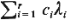
However, we can maximize the expected rate of growth of the "cost outflow" curve
by always
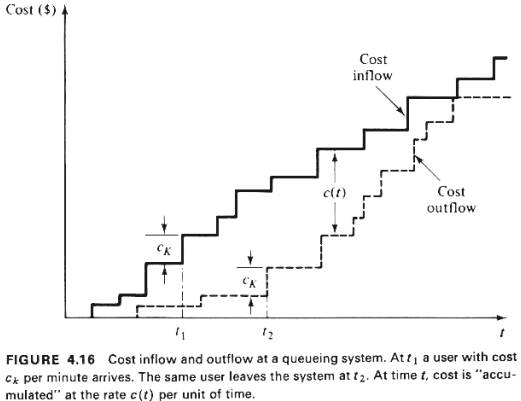
selecting among the available users the one that "expels"
expected cost from the system at the maximum rate per unit of time. This is equivalent to
choosing the user with the maximum ck· k, (= rate of
cost "expulsion" per unit time resulting from serving a user of class k) which
confirms the theorem. It should also be noted that the first of the two terms on the
right-hand side of (4.109) is a constant that is independent of the priority assignments.
Therefore, to minimize (4.109) one must minimize the second sum on the right.
The following corollary follows from the theorem.
Corollary: To minimize the average waiting time for all users in
the system, assign priorities according to the expected service times for each user class:
the shorter the expected service time, the higher the priority of the class.
To prove the corollary, all we have to do is
set ck = 1 for all k in the theorem (this is equivalent
to assigning equal weight to a unit of time's waiting for all classes of users). Then
fk=k, and the result of the corollary
follows.
The corollary we have just discussed is
sometimes referred to as the 'Ishortest-expected-processing-time-first" (SEPT)
rule. Note that, contrary to FCFS, SIRO, and LCFS, SEPT
affects the distribution of the number of users present in the queueing system and the
expected waiting and total system times by using a characteristic of the length of service
time as the criterion for sequencing.
|
