4.9.3 Nonpreemptive Priorities in a M/M/m System
In attempting to extend expressions such as
(4.107) to the case of queueing systems with many servers, one encounters the same
problems that arise in trying to extend the analysis of M/G/1 queueing systems to M/G/m
queueing systems. Thus, exact results for multiserver queueing systems with nonpreemptive
priorities are available only for the case of negative exponential
service times (M/M/m systems). Moreover, the mathematical analysis becomes intractable
unless all r priority classes of users have the same mean service time,  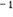 . .
Under these assumptions-and using the same
notation as for the singleserver system-it is not difficult to show (see Problem 4.8)
that, as before,
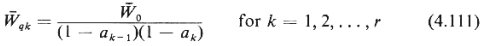
where  0, is now defined as the expected
value of the remaining time until any one of the m servers becomes free following
the arrival of a new user (of class k) at the queueing system.12
(If one or more of the servers are free at the instant of the new arrival, that
remaining time is equal to zero.) From the theory of M/M/m queueing systems and, in
particular, from expresion 0, is now defined as the expected
value of the remaining time until any one of the m servers becomes free following
the arrival of a new user (of class k) at the queueing system.12
(If one or more of the servers are free at the instant of the new arrival, that
remaining time is equal to zero.) From the theory of M/M/m queueing systems and, in
particular, from expresion
(4.44), we then have (assuming 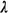 1 + 1 + 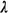 2
+ . . . + 2
+ . . . + 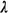 r
< m r
< m ) )
 0
= P{all servers are busy}. E[remaining time | all servers are busy] 0
= P{all servers are busy}. E[remaining time | all servers are busy]
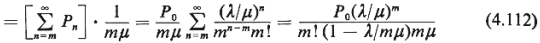
where P0 is given by (4.46) and 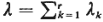 . .
This queueing model-and expression (4.111)-is
among the most applicable in urban operations research. Many urban services can be viewed
as multiserver systems with Poisson demands of several types and with (nonpreemptive)
priority rules that determine the order in which different types of demands will be
serviced. In fact, the model places no restrictions on how the types of demand will be
defined. Thus, one can, for instance, classify demands according to the region of a city
from which they originate or according to the type of service requested or both (e.g., 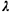 ij,
might be the rate at which j-alarm fires are generated from region i in
a city). ij,
might be the rate at which j-alarm fires are generated from region i in
a city).
The most restrictive assumption in the model is
that service times to all types of demands are assumed to be identical, negative
exponential random variables, but even in cases when this is not quite true, expression
(4.111) can still be used to obtain some idea of the level of delay experienced by
different types of demands for various priority rankings and for different values of m
(see also Chapter 5 in [LARS 72b]).
12 As usual for multiserver systems, we define 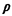 i = i = 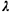 i/ m i/ m
|