|
5.13 Server-dependent mean service times Suppose that
in the three-server example of Section 5.4.3 we were told that the mean
service times of the various servers were not identical, but were given
as follows:  1-1 = 2/3, 1-1 = 2/3,  2-1 = 1.0, and 2-1 = 1.0, and  3-1 = 2.0(units of time). Here 3-1 = 2.0(units of time). Here
 includes both travel time and on-scene time. includes both travel time and on-scene time.
- Determine a requirement for A such that the system is not
saturated (i.e., that the total required service does not exceed the
total available capacity).
- Assuming that
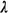 = 1.5, write a set of
balance-of-flow equations analogous to (5.22)-(5.29) whose solutions
yield the system equilibrium state probabilities. = 1.5, write a set of
balance-of-flow equations analogous to (5.22)-(5.29) whose solutions
yield the system equilibrium state probabilities.
Hint: This system, when unsaturated, does not collapse to an M
/ M / 3 birth-and-death model, so one does not know the sums of
probabilities along certain hyperplanes.
- Suppose we are given a numerical value for
P111. Find PQ in terms of
P111 [see (5.21e)].
Hint: The system is a birth-and-death process for saturated
system states.
- Argue that (5.30) for server workloads and (5.32) for
"unsaturated" interatom dispatch frequencies remain unchanged.
- Argue that (5.34) should be replaced with

Conclude that (5.36), (5.37), and (5.38) remain unchanged, assuming
that fnj[2], as given by (*), is
substituted for 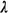 jP'Q/ jP'Q/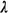 N in (5.35). N in (5.35).
- Mean travel times are more difficult and require
approximations. Can you fill in the details?
|



