5.14 Interdistrict dispatching, revisited In Section 5.6 we found that for a nontime-varying system with 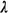_n(t) = _n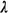, _n(t) = _n, the fraction of dispatches that are interdistrict dispatches is

1. Examine the special case _n = , and physically interpret your result.

2. Examine the special case 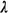_n constant, and physically interpret your result.

3. In the text we developed (5.55), allowing for a time-varying system in which the sector car is always given first preference. However, for a system in which the dispatcher has car location information, he may prefer to assign an out-of-sector car that is closer to the scene than the sector car. Our previous analysis can be generalized to allow for this type of behavior. Let

   an(t) =

   probability that unit n is assigned to a call that arrives from sector n at time t, given that unit n is available

   Derive the analogous result to (5.55) for this more general model. What are the physical implications of the result?

4. Does the practical significance of the results above change if we allow a queue to form? As a guide to answering this question, consider a nontime-varying system in near-saturation conditions (i.e., a queue almost always exists). A call that arrives when all N servers are busy is entered in queue. The queue is depleted in a first-come, first-served manner. Prove that