5.3Coverage problem Consider a circular roadway in an urban region as shown in Figure P5.3. The roadway has many shops, entertainment spots, and other potential targets for crime. The patrol cars of the city's police department are all unmarked and thereby provide no visible police coverage (protection) while patrolling. However, when they are stopped at a scene of a call for service, they flash a beacon that is visible (in either direction) for exactly a miles (a << 1.0). Thus, each parked patrol car generates a region of visible police coverage of length 2a miles.

The total number of patrol cars is so great, and the priority of calls on the circular roadway so urgent, that no call for service from the circular roadway is ever delayed in queue. And travel time to the scene for a call for service is insignificant compared to the service time at the scene, which has a mean 1/.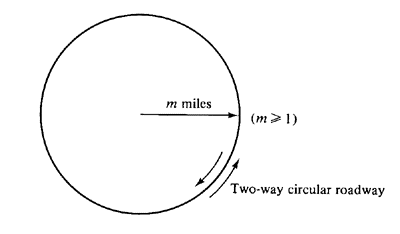

Calls for police service along the circular roadway arrive as a Poisson process with an average rate of calls per linear mile. We assume that the system is operating in the steady state.

Show that, in the steady state, the expected length (in miles) of the circular roadway that is given visible police coverage is equal to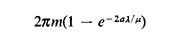