|
5.4 Testing your understanding of the two-server model
Consider the city depicted in Figure P5.4. In this city emergency repair
service is provided by two response units, prepositioned at (1, 0) and
(-1, 0), respectively. Travel distance is right angle, with distance
d between two points (x1, y1)
and (x2, y2) equal to

Repairs occur according to a spatial and temporal Poisson process
with

Unit 1's primary response area consists of all points east of the
north-south boundary line that partitions the city. Unit 2's primary
response area consists of all points west of that line. Note that the
boundary, as drawn, is an equal travel-time boundary line. Whenever an
emergency repair is reported from response area i (i = 1,
2), unit i is assigned, if available;
otherwise, the other unit is assigned, if
available. If neither unit is available, the call is lost (i.e.,
no queueing is allowed).
Repair units travel at 100 miles/hr to and from the scene. On-scene
service time is negative exponential with mean  -1 = 10 hours. Upon completion of service,
a unit always returns to its home location. Finally, -1 = 10 hours. Upon completion of service,
a unit always returns to its home location. Finally, 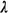 o = 2 x 10-5 (emergencies per
hour per square mile). Assume the system is operating in steady state.
Average system-wide travel time to an emergency is o = 2 x 10-5 (emergencies per
hour per square mile). Assume the system is operating in steady state.
Average system-wide travel time to an emergency is 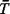 . .
- Using suitable approximations, or exact analysis if you prefer,
find approximate nonzero values for
 1
and 1
and  2, where 2, where  m m 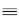 workload of unit m.
workload of unit m.
- The random variable Dx is defined to be the
system-wide east-west (or west-east) travel distance for a random
emergency. Sketch the pdf for Dx, again making
suitable approximations.
- Approximately, what is the fraction of dispatches that are
interresponse area dispatches?
For parts (d)-(g) only, suppose that 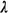 o = 10-2. This yields new
values for o = 10-2. This yields new
values for  1, 1,  2, 2, 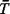 , and so on.
In considering each of these questions [parts (d)-(g)], assume that the
total service-time distribution remains the same as that assumed in
parts (a)-(c). , and so on.
In considering each of these questions [parts (d)-(g)], assume that the
total service-time distribution remains the same as that assumed in
parts (a)-(c).
- Suppose the equal-travel-time boundary line is shifted a distance
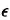 ( (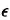 small) toward
unit 1. Which is the appropriate response? small) toward
unit 1. Which is the appropriate response?
- As a result of the shift,
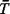 will increase
but | will increase
but | 1 - 1 -  2| will decrease. 2| will decrease.
- As a result of the shift,
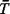 will increase
and | will increase
and | 1 - 1 -  2| will increase. 2| will increase.
- As a result of the shift,
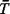 will decrease
and | will decrease
and | 1 - 1 -  2| will decrease. 2| will decrease.
- As a result of the shift,
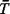 will decrease
but | will decrease
but | 1 - 1 -  2| will increase. 2| will increase.
- As a result of the shift, we cannot tell which of the four
possibilities above will apply.
- Now suppose that the equal-travel-time boundary line is shifted a
distance
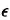 ( (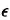 small) toward unit 2. Dy is defined to be the
system-wide north-south (or south-north) travel distance for a random
emergency. As a result of the shift,
small) toward unit 2. Dy is defined to be the
system-wide north-south (or south-north) travel distance for a random
emergency. As a result of the shift,
- E[Dy] will stay the same.
- E[Dy] will increase.
- E[Dy] will decrease.
- The behavior of E[Dy] cannot be
determined.
- As in part (e), suppose that the equal-travel-time boundary line
is shifted a distance
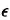 ( (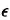 small) toward unit 2. As a result of the shift: small) toward unit 2. As a result of the shift:
- (
 1 + 1 +  2) will stay the same. 2) will stay the same.
- (
 1 + 1 +  2) will increase. 2) will increase.
- (
 1 + 1 +  2) will decrease. 2) will decrease.
- The behavior of (
 1 + 1 +  2) cannot be determined. 2) cannot be determined.
- Suppose that a third unit is added as a backup unit and is
located at (x = 0, y = 0). This unit is assigned to any
emergency that occurs when both units 1 and 2 are busy and unit 3 is
available. Emergencies that arrive when all three units are busy are
lost. Determine the workload of unit 3,
 3. 3.
|




