A good answer might be:

Since u · v  =  |u||v| cos θ and all vectors in this problem have length 1.0, u · v  =  cos θ.

The dot product of au · bu  is the cosine of the angle between au and bu, which can be read off the diagram as 0.866.

The dot product of au · cu  is the cosine of the angle between au and cu, which can be read off the diagram as 0.500.


Filtering out the effect of Length

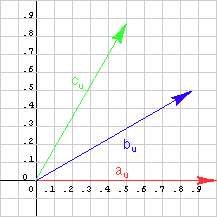
bu is closer in orientation to au; so au · bu is the larger.

au is (1, 0)       --- a unit vector at zero degrees
bu is (0.866, 0.5)  --- a unit vector at 30 degrees
cu is (0.5, 0.866)  --- a unit vector at 60 degrees

Remember: cos 30°   =  0.866, sin 30°   =  0.5,
cos 60°   =  0.5, and sin 60°   =  0.866.
The dot products are:

au · bu  is 0.866
au · cu  is 0.500

So by using vectors of length one, the effect of length is removed and the dot product is larger when a small angle separates the vectors.


QUESTION 5:

What do you suppose happens when the vectors are in opposite directions, such as (1, 0)T and (-1, 0)T ?