 A DSP-based decompressor
unit for high-fidelity MPEG-Audio over TCP/IP networks
A DSP-based decompressor
unit for high-fidelity MPEG-Audio over TCP/IP networks A DSP-based decompressor
unit for high-fidelity MPEG-Audio over TCP/IP networks
A DSP-based decompressor
unit for high-fidelity MPEG-Audio over TCP/IP networks[ Home | Contents | Component and tool archive ]
Previous chapter: Introduction, next chapter: Digital Signal Processing
Audio is equal to air pressure changes, which happen continously both in time and in amplitude. In order to store such a signal in a computer, it needs to be discretized both in the time-domain and in the amplitude-domain, and this is called sampling the signal. The human ear can perceive frequencies between 20hz and 20khz. According to the Nyquist theorem, you need to sample a signal at twice the maximum bandwidth to avoid aliasing distortions. To allow for imperfect filters, the sampling frequency of 44.1kHz is used in current digital consumer HiFi-products like CD-players. Professional applications typically use a 48kHz samplerate.
To produce a digital version of each sample, the signal amplitude has to be sampled and quantized into a binary value. If the quantization is very coarse (low number of bits used), the reconstructed audio signal will differ audibly from the original signal. The noise introduced by quantization is called, appropriately, quantization noise, and sets the maximum signal-to-noise ratio that can be achieved (other factors like input filters and analog processing stages always creates some additional noise). The S/N ratio is usually expressed in decibels (dB) and is defined as S/N = 10log(sqr(Vsignal)/sqr(Vnoise)) = 20log(Vsignal/Vnoise). The quantization noise strength is one bit, which means that each additional bit used in the digitalization process, adds approximately 20log(2)=6 dB to the s/n ratio. Compact Disc's are recorded with 16 bits, and achieves a maximum s/n ratio of 96 dB. Professional applications might use 18 or 20 bits instead, to achieve even higher s/n ratios. The sample values are typically stored in linear form or in a logarithmic form (called u-law or A-law). The latter increases the possible dynamic range (but adds more noise, of course).
Sampling a stereo signal at 44 kHz using 16 bits per sample, requires a bit-rate of 1.4 megabits. Even with modern networks and harddisks, this amount of data is too large to be comfortably stored and retrieved, if you are going to use or work with more than some minutes of audio.
Typical loss-less data compression methods involve the detection of repeated sequences of data, and statistically recoding frequently occuring symbols into shorter symbols. This works well for text, computer programs and other data-streams that has a high degree of temporal redundancy. However, data like audio and pictures, cannot be compressed to very high degrees using conventional methods. A typical sampled audio-file compressed using a normal repeated-sequence compressor like PKZIP or gzip, results in a reduction in length by only 10-15%, which is far too low to be of any use. Therefore, many lossy compression methods for digital audio have been developed, with a very varying amount of audible loss. These can be divided into those operating in the time-domain, and those operating in the frequency-domain (with associated transforms back and forth).
One common method, is to calculate and quantize the differences between consequitive samples, or between the next sample and a prediction of the next sample, instead of the samples themselves. Hopefully, this difference/error term will be smaller and more adept to quantizing than the original sample values. These coding methods have the common name DPCM, Differential Pulse Code Modulation. They can be improved by adapting the prediction to the current signal characteristics and one such scheme is called ADPCM, which means Adaptive Differential Pulse Code Modulation, and can compress speech to between 16 and 40kbit/s depending on quality desired.
Another way is to model the vocal-tract and map speech to the mathematical model, then just transfer coefficients for the model instead of the actual sample values. These compressors are called vocoders, and an example is LPC, Linear Predictive Coding. This results in a bitstream using only 2.4 kbit/s, but it is very lossy and sounds very synthetic and metallic. An extension to LPC is CELP, Code Excited Linear Predictor, which does what LPC does but also tries to transmit as much of the error term as possible, under the given bit-rate restrictions. Decent phone-line quality audio can be obtained using CELP at a bitrate of 4.8 kbit/s.
Much better compression ratios of high-quality audio have been obtained using compressors working in the frequency domain, called subband-coders. This is because audio is fundamentally composed of superimposed frequencies of different energies, and thus it is easier to find redundancies and localise information that can be discarded without audible loss, if the compression scheme operates in the frequency domain. Quantization noise added when reducing the number of bits a band is transmitted with, is contained within that frequency band. There are many different frequency-domain audio compressing standards, but the most successful of them share the same underlying principle, the principle that has been dubbed psychoacoustics.
Human hearing is a magnificient system, with a dynamic range of over 96dB. However, it is apparent that while we can easily hear a very silent noise like a needle falling, and a very loud noise like an aeroplane taking off, it is impossible to discern the falling needle if we hear the aeroplane at the same time. The hearing system adapts to dynamic variations in the sounds, and these adaptions and masking effects form the basics of the psychoacoustic theories and research.
In a similar but more subtle manner as in the example above, schemes for noise-reduction in taperecordings were developed several years ago. They used the fact that while it is easy to hear tape-hiss and noise in silent passages in the music, it is much harder to discern it in loud passages - the noise is psychoacoustically masked by the louder sounds. Since then many studies have been made to get a better understanding on how a loud sound can mask more silent sounds, both in the frequency and time domain.
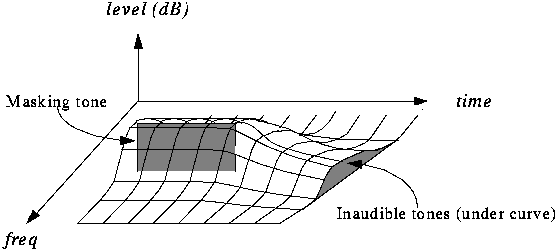
As can be seen in the figure, a masking effect occurs around strong sounds. Noise, or silent sounds in the spatial and temporal vicinity cannot be discerned by our hearing if it lies below the threshold curve. This is the observation that is the foundation of psychoacoustic compression - that it is allowed to permit more noise in sounds close to strong masking sounds. Adding noise in sampling contexts is the same as quantizing coarser (using less bits to transmit a value) and that is the same as compression.
The trick is of course to find an algorithm that can reliably tell the compressor which sounds can be transferred with more noise. Generally, these compressors work by transforming the sampled signal into the frequency domain, then applying psychoacoustics, quantizing each frequency band and sending. The decompressor only has to turn the transmitted frequency bands back into the time-domain.
There are two major, non-proprietary standards that work using these principles - Dolby AC and MPEG-Audio. Both of these specify several schemes with different complexity and efficiency. The most advanced schemes are Dolby AC-3 and MPEG-1 Layer-3, and they are very similar to each other but AC-3 is optimized for multi-channel encoding of movie soundtracks etc, so for normal stereo audio signals, MPEG is more efficient. Since multichannel surround sound lies beyond the scope of this thesis, MPEG-1 Layer-3 compression of audio was chosen as the algorithm to be used.
The MPEG-1 audio standard, ISO/IEC 11172-3, defines three layers of increasing complexity and compression efficiency. Each layer extends the former, but adds features that allow for better sound at lower bitrates. Common to all three layers is a transform into the frequency domain, a psychoacoustic analysis, and a quantizer that creates the bitstream. However, what the standard actually defines, is the bitstream format, thus implying a defined decoder. The standard does not define the details of the encoding process, but merely suggests encoding methods. A small overview of the three defined audio layers will follow, but details about the encoding process will not be covered in this paper.
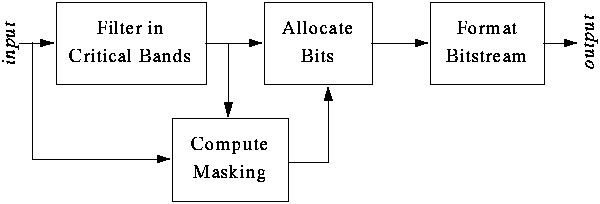
The audio samples are first fed into a filterbank, which transforms the signal into frequency bands. The filterbanks are critically sampled, which means that there are as many samples in the time-domain as in the frequency domain. Hence if the signal had not been quantized later, perfect reconstruction would be possible. Meanwhile, a psychoacoustic model analyses the audio samples to find the best set of quantization levels to use for encoding each frequency band. The frequency band levels are fed into the quantizer and bit allocator, which uses the psychoacoustical analysis to perform a quantization of the band energies, and a bitstream formatting matching the chosen encoding layer. The bitstream includes the compressed data, and side-information telling the decoder how the data was compressed (there are numerous options and choices available for the encoder to choose for each frame). Exactly how the psychoacoustical model works and how it controls the quantizer, is up to the encoder designer to choose, and is where proprietary algorithms fit into an otherwise non-proprietary standard. Finally, the bitstream is packed together with ancillary data (if any) into frames, which form the output of the encoder.
Depending on performance requirements, different layers can be choosed. Higher-numbered layers add features which increase performance, but also increases complexity in both the encoder and the decoder. A layer-N decoder is capable of decoding layers 1 to N.
Layer-1 implements the most fundamental scheme. The filterbank operates on 64 samples at a time, with 50% overlap, creating 32 frequency bands at a time from 32 audio samples input. The frequency bands are assembled into quantization blocks in a fixed manner (the bands do not correspond to the critical band boundaries of psychoacoustics), and a simple psychoacoustic model with fixed band boundaries assigns bits to the quantizer so it can quantize and format the band energies. Layer-2 extends layer-1 with additional bit-allocation techniques, while layer-3 adds many things including 18-doubled frequency resolution thanks to a hybrid filterbank with 576 bands, non-uniform quantizing of band energies, adaptive segmentation of quantization bands according to psychoacoustics, and entropy-coding of the resulting data (huffman coding). Layer-3's psychoacoustics also take the temporal masking effects into consideration, and features an adaptive transform length that can switch the transforms to short blocks when it detects strong transients in the signal, and thereby increasing the temporal resolution for the transients. Without this technique, the transient would be smoothed out due to the comparatively large block size.
The decompressed signals quality is currently impossible to assess using technical terms as S/N ratio or distortion, since all lossy compression schemes might add these even though they are not perceptible. Therefore, subjective listening tests are performed where the subjects rate a compressed/decompressed signal compared to the original signal. According to the Fraunhofer institute, who developed the MPEG-1 Audio layer-3 standard, the achieved compression ratios while maintaining a "near CD-quality" sound for the three layers at a sampling frequency of 44.1kHz are:
| Layer | Approximate Ratio | Resulting stereo bitrate |
| 1 | 1:4 | 384kbit/s |
| 2 | 1:6-1:8 | 256-192kbit/s |
| 3 | 1:10-1:12 | 128-112kbit/s |
This means that a "near CD-quality" stereo audio stream compressed using MPEG Audio Layer-3 would only need a speed of 128kbit/s, which is very little compared to traditional LAN's speed of 10-100Mbit/s, and matching the speed of ISDN at 128kbit/s.
Additional references:
Previous chapter: Introduction, next chapter: Digital Signal Processing
This document may be freely distributed for educational purposes. See the copyright notice for additional information.