Exercises

1. Suppose we know a priori that a given key is equally likely to be any integer between a and b.
   1. When is the division method of hashing a good choice?
   2. When is the middle square method of hashing a good choice?
2. Compute (by hand) the hash value obtained by Program  for the strings "ece.uw.ca" and "cs.uw.ca". Hint: Refer to Appendix .
3. Canadian postal codes have the format LDL DLD where L is always a letter (A-Z), D is always a digit (0-9), and is always a single space. E.g., the postal code for the University of Waterloo is N2L 3G1. Devise a suitable hash function for Canadian postal codes.
4.   For each type of hash table listed below, show the hash table obtained when we insert the keys

   

   in the order given into a table of size M=16 that is initially empty. Use the following table of hash values:

   x	Hash(x) (octal)
   "un"	016456
   "deux"	0145446470
   "trois"	016563565063
   "quatre"	010440656345
   "cinq"	0142505761
   "six"	01625070
   "sept"	0162446164
   "huit"	0151645064
   "neuf"	0157446446
   "dix"	01455070
   "onze"	0156577345
   "douze"	014556647345

   1. chained hash table,
   2. chained scatter table,
   3. open scatter table using linear probing,
   4. open scatter table using quadratic probing, and
   5. open scatter table using double hashing. (Use Equation  as the secondary hash function).
5. For each table obtained in Exercise , show the result when the key "deux" is withdrawn.
6. For each table considered in Exercise  derive an expression for the total memory space used to represent a table of size M that contains n items.
7. Consider a chained hash table of size M that contains n items. The performance of the table decreases as the load factor increases. In order to keep the load factor below one, we propose to double the size of the array when n=M. However, in order to do so we must rehash all of the elements in the table. Explain why rehashing is necessary.
8. Give the sequence of M keys that fills a chained scatter table of size M in the shortest possible time. Find a tight, asymptotic bound on the minimum running time taken to fill the table.
9. Give the sequence of M keys that fills a chained scatter table of size M in the longest possible time. Find a tight, asymptotic bound on the minimum running time taken to fill the table.
10. Consider the chained hash table implementation shown in Programs , , and .
    1. Rewrite the Insert routine so that it doubles the length of the array when .
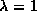    2. Rewrite the Withdraw routine so that it halves the length of the array when .
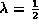    3. Show that the average time for both insert and withdraw operations is still O(1).
11. Consider two sets of integers, and .
    1. Devise an algorithm that uses a hash table to test whether S is a subset of T. What is the average running time of your algorithm?
    2. Two sets are equivalent if and only if both 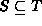and 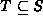. Show that we can test if two sets of integers are equivalent in O(m+n) time (on average).
12.   (This question should be attempted after reading Chapter ). Rather than use an array of linked lists, suppose we implement a hash table with an array of binary search trees.
    1. What are the worst-case running times for Insert, Find and Withdraw.
    2. What are the average running times for Insert, Find and Withdraw.
13.   (This question should be attempted after reading Section ). Consider a scatter table with open addressing. Devise a probe sequence of the form

    

    where c(i) is a full-period pseudo random number generator. Why is such a sequence likely to be better than either linear probing or quadratic probing?

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.