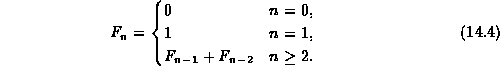
The Fibonacci numbers are given by following recurrence
Section ![]() presents a recursive function to compute
the Fibonacci numbers by implementing directly Equation
presents a recursive function to compute
the Fibonacci numbers by implementing directly Equation ![]() .
(See Program
.
(See Program ![]() ).
The running time of that program is shown to be
).
The running time of that program is shown to be ![]() .
.
In this section we present a divide-and-conquer style of algorithm for computing Fibonacci numbers. We make use of the following identities
![]()
for ![]() .
(See Exercise
.
(See Exercise ![]() ).
Thus, we can rewrite Equation
).
Thus, we can rewrite Equation ![]() as
as
Program ![]() defines the function Fibonacci which
implements directly Equation
defines the function Fibonacci which
implements directly Equation ![]() .
Given n>1 it computes
.
Given n>1 it computes ![]() by calling itself recursively
to compute
by calling itself recursively
to compute ![]() and
and ![]() and then combines the two results as required.
and then combines the two results as required.

Program: Divide-and-Conquer Example--Computing Fibonacci Numbers
To determine a bound on the running time of the Fibonacci routine
in Program ![]() we assume that T(n) is a non-decreasing function.
I.e.,
we assume that T(n) is a non-decreasing function.
I.e., ![]() for all
for all ![]() .
Therefore
.
Therefore ![]() .
Although the program works correctly for all values of n,
it is convenient to assume that n is a power of 2.
In this case, the running time of the routine is upper-bounded by T(n)
where
.
Although the program works correctly for all values of n,
it is convenient to assume that n is a power of 2.
In this case, the running time of the routine is upper-bounded by T(n)
where
Equation ![]() is easily solved using repeated substitution:
is easily solved using repeated substitution:
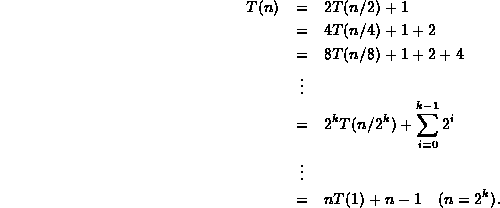
Thus, T(n)=2n-1=O(n).