In this section we examine some of the mathematical properties of big oh.
In particular, suppose we know that ![]() and
and ![]() .
.
The first theorem addresses the asymptotic behavior of the sum of two functions whose asymptotic behaviors are known:
Theorem Ifand
, then
extbfProof
By Definition ![]() , there exist two integers,
, there exist two integers, ![]() and
and ![]() and two constants
and two constants ![]() and
and ![]() such that
such that
![]() for
for ![]() and
and
![]() for
for ![]() .
.
Let ![]() and
and ![]() .
Consider the sum
.
Consider the sum ![]() for
for ![]() :
:
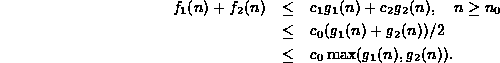
Thus, ![]() .
.
According to Theorem ![]() ,
if we know that functions
,
if we know that functions ![]() and
and ![]() are
are
![]() and
and ![]() , respectively,
the sum
, respectively,
the sum ![]() is
is ![]() .
The meaning of
.
The meaning of ![]() is this context is
the function h(n) where
is this context is
the function h(n) where ![]() for integers all
for integers all ![]() .
.
For example, consider the functions ![]() and
and
![]() .
Then
.
Then
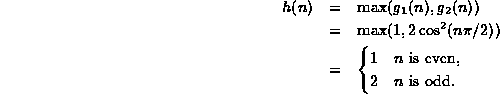
Theorem ![]() helps us simplify the asymptotic analysis
of the sum of functions by allowing us to drop the
helps us simplify the asymptotic analysis
of the sum of functions by allowing us to drop the ![]() required by Theorem
required by Theorem ![]() in certain circumstances:
in certain circumstances:
Theorem Ifin which
and
are both non-negative for all integers
such that
for some limit
, then
.
extbfProof According to the definition of limits , the notation
![]()
means that, given any arbitrary positive value ![]() ,
it is possible to find a value
,
it is possible to find a value ![]() such that for all
such that for all ![]()
![]()
Thus, if we chose a particular value, say ![]() ,
then there exists a corresponding
,
then there exists a corresponding ![]() such that
such that
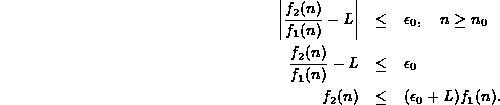
Consider the sum ![]() :
:
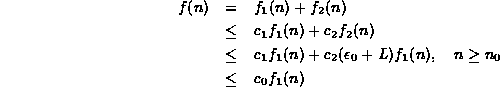
where ![]() .
Thus,
.
Thus, ![]() .
.
Consider a pair of functions ![]() and
and ![]() ,
which are known to be
,
which are known to be ![]() and
and ![]() , respectively.
According to Theorem
, respectively.
According to Theorem ![]() ,
the sum
,
the sum ![]() is
is ![]() .
However, Theorem
.
However, Theorem ![]() says that,
if
says that,
if ![]() exists,
then the sum f(n) is simply
exists,
then the sum f(n) is simply ![]() which,
by the transitive property (see Theorem
which,
by the transitive property (see Theorem ![]() below), is
below), is ![]() .
.
In other words, if the ratio ![]() asymptotically approaches a constant as n gets large,
we can say that
asymptotically approaches a constant as n gets large,
we can say that ![]() is
is ![]() ,
which is often a lot simpler than
,
which is often a lot simpler than ![]() .
.
Theorem ![]() is particularly useful result.
Consider
is particularly useful result.
Consider ![]() and
and ![]() .
.

From this we can conclude that ![]() .
Thus, Theorem
.
Thus, Theorem ![]() suggests that
the sum of a series of powers of n is
suggests that
the sum of a series of powers of n is ![]() ,
where m is the largest power of n in the summation.
We will confirm this result in Section
,
where m is the largest power of n in the summation.
We will confirm this result in Section ![]() below.
below.
The next theorem addresses the asymptotic behavior of the product of two functions whose asymptotic behaviors are known:
Theorem Ifand
, then
extbfProof
By Definition ![]() , there exist two integers,
, there exist two integers, ![]() and
and ![]() and two constants
and two constants ![]() and
and ![]() such that
such that
![]() for
for ![]() and
and
![]() for
for ![]() .
Furthermore, by Definition
.
Furthermore, by Definition ![]() ,
,
![]() and
and ![]() are both non-negative for all integers
are both non-negative for all integers ![]() .
.
Let ![]() and
and ![]() .
Consider the product
.
Consider the product ![]() for
for ![]() :
:
![]()
Thus, ![]() .
.
Theorem ![]() describes a simple,
but extremely useful property of big oh.
Consider the functions
describes a simple,
but extremely useful property of big oh.
Consider the functions ![]() and
and
![]() .
By Theorem
.
By Theorem ![]() ,
the asymptotic behavior of the product
,
the asymptotic behavior of the product ![]() is
is ![]() .
I.e., we are able to determine the asymptotic behavior of
the product without having to go through the gory details of
calculating that
.
I.e., we are able to determine the asymptotic behavior of
the product without having to go through the gory details of
calculating that ![]() .
.
The next theorem is closely related to the preceding one in that it also shows how big oh behaves with respect to multiplication.
Theorem Ifand
is a function whose value is non-negative for integers
, then
extbfProof
By Definition ![]() , there exist integers
, there exist integers ![]() and constant
and constant ![]() such that
such that
![]() for
for ![]() .
Since
.
Since ![]() is never negative,
is never negative,
![]()
Thus, ![]() .
.
Theorem ![]() applies when we multiply a function,
applies when we multiply a function, ![]() ,
whose asymptotic behavior is known to be
,
whose asymptotic behavior is known to be ![]() ,
by another function
,
by another function ![]() .
The asymptotic behavior of the result is simply
.
The asymptotic behavior of the result is simply ![]() .
.
One way to interpret Theorem ![]() is that it allows us to do the following mathematical manipulation:
is that it allows us to do the following mathematical manipulation:
![]()
I.e., Fallacy ![]() notwithstanding,
we can multiply both sides of the ``equation'' by
notwithstanding,
we can multiply both sides of the ``equation'' by ![]() and the ``equality'' still holds.
Furthermore, when we multiply
and the ``equality'' still holds.
Furthermore, when we multiply ![]() by
by ![]() ,
we simply bring the
,
we simply bring the ![]() inside the
inside the ![]() .
.
The last theorem in this section introduces the transitive property of big oh:
Theorem (Transitive Property) If f(n)=O(g(n)) and g(n)=O(h(n)) then f(n)=O(h(n)).
extbfProof
By Definition ![]() , there exist two integers,
, there exist two integers, ![]() and
and ![]() and two constants
and two constants ![]() and
and ![]() such that
such that
![]() for
for ![]() and
and
![]() for
for ![]() .
.
Let ![]() and
and ![]() . Then
. Then

Thus, f(n)=O(h(n)).
The transitive property of big oh
is useful in conjunction with Theorem ![]() .
Consider
.
Consider ![]() which is clearly
which is clearly ![]() .
If we add to
.
If we add to ![]() the function
the function ![]() ,
then by Theorem
,
then by Theorem ![]() ,
the sum
,
the sum ![]() is
is ![]() because
because ![]() .
I.e.,
.
I.e., ![]() .
The combination of the fact that
.
The combination of the fact that ![]() and the transitive property of big oh,
allows us to conclude that the sum is
and the transitive property of big oh,
allows us to conclude that the sum is ![]() .
.