|
Data Structures and Algorithms
with Object-Oriented Design Patterns in C# |
In this section we present a technique for solving a recurrence
relation such as Equation ![]() called
repeated substitution .
The basic idea is this:
Given that
called
repeated substitution .
The basic idea is this:
Given that ![]() ,
then we may also write
,
then we may also write ![]() , provided n>1.
Since T(n-1) appears in the right-hand side of the former equation,
we can substitute for it the entire right-hand side of the latter.
By repeating this process we get
, provided n>1.
Since T(n-1) appears in the right-hand side of the former equation,
we can substitute for it the entire right-hand side of the latter.
By repeating this process we get
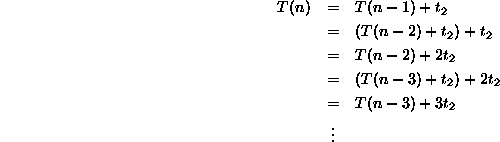
The next step takes a little intuition: We must try to discern the pattern which is emerging. In this case it is obvious:
![]()
where ![]() .
Of course, if we have doubts about our intuition,
we can always check our result by induction:
.
Of course, if we have doubts about our intuition,
we can always check our result by induction:
extbfProof (By Induction).
Base Case
Clearly the formula is correct for k=1,
since ![]() .
.
Inductive Hypothesis
Assume that ![]() for
for ![]() .
By this assumption
.
By this assumption
Note also that using the original recurrence relation we can write
for ![]() .
Substituting Equation
.
Substituting Equation ![]() in the right-hand side of Equation
in the right-hand side of Equation ![]() gives
gives
![]()
Therefore, by induction on l, our formula is correct
for all ![]() .
.
So, we have shown that ![]() , for
, for ![]() .
Now, if n was known,
we would repeat the process of substitution until we got T(0)
on the right hand side.
The fact that n is unknown should not deter us--we get T(0) on the right hand side when n-k=0.
That is, k=n.
Letting k=n we get
.
Now, if n was known,
we would repeat the process of substitution until we got T(0)
on the right hand side.
The fact that n is unknown should not deter us--we get T(0) on the right hand side when n-k=0.
That is, k=n.
Letting k=n we get
where ![]() and
and
![]() .
.