![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
Next: 11.2 Vector Reduction
Up: 11 Hypercube Algorithms
Previous: 11 Hypercube Algorithms
Recall from Section 3.7.2 that a hypercube connects
each of P
tasks ( P
a power of 2) to 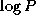 other tasks
(Figure 3.16). The template considered in this
chapter uses this communication structure in an SPMD fashion, with
each task executing Algorithm 11.1. A local state
variable is first set to be the supplied input data. Computation then
proceeds in
other tasks
(Figure 3.16). The template considered in this
chapter uses this communication structure in an SPMD fashion, with
each task executing Algorithm 11.1. A local state
variable is first set to be the supplied input data. Computation then
proceeds in 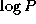 steps. In each step, each task first exchanges
its local state with one of its neighbors in the hypercube and
then combines the message received from the neighbor with
state to generate a new state. The output of the computation
is the state generated in the final step.
steps. In each step, each task first exchanges
its local state with one of its neighbors in the hypercube and
then combines the message received from the neighbor with
state to generate a new state. The output of the computation
is the state generated in the final step.

In Algorithm 11.1, the XOR function denotes an
exclusive or operation and is used to identify neighbors. (Exclusive
or is defined as follows: 0 XOR 0=0, 0 XOR 1=1, 1 XOR
0=1, 1 XOR 1=0.) As noted in Section 3.7.2, the
hypercube has the property that the binary labels of two nodes that
are neighbors in the
d
th dimension differ only in the d
th place; hence, the
expression myid XOR 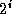 yields the i
th neighbor of node
myid.
yields the i
th neighbor of node
myid.
A particular parallel algorithm is defined by the operator OP
used to combine state and message at each step in the
template. In the following, we shall show how this template can be
used as a basis for parallel vector reduction, matrix transposition,
and sorting algorithms.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
Next: 11.2 Vector Reduction
Up: 11 Hypercube Algorithms
Previous: 11 Hypercube Algorithms
© Copyright 1995 by Ian Foster
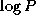 other tasks
(Figure 3.16). The template considered in this
chapter uses this communication structure in an SPMD fashion, with
each task executing Algorithm 11.1. A local state
variable is first set to be the supplied input data. Computation then
proceeds in
other tasks
(Figure 3.16). The template considered in this
chapter uses this communication structure in an SPMD fashion, with
each task executing Algorithm 11.1. A local state
variable is first set to be the supplied input data. Computation then
proceeds in 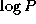 steps. In each step, each task first exchanges
its local state with one of its neighbors in the hypercube and
then combines the message received from the neighbor with
state to generate a new state. The output of the computation
is the state generated in the final step.
steps. In each step, each task first exchanges
its local state with one of its neighbors in the hypercube and
then combines the message received from the neighbor with
state to generate a new state. The output of the computation
is the state generated in the final step.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)

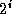 yields the i
th neighbor of node
myid.
yields the i
th neighbor of node
myid.