![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
At this point, we have presented all the HPF features needed to write simple programs. Array assignment statements provide a mechanism for specifying fine-grained concurrency, while data distribution directives provide control over agglomeration and mapping.
The F90 array assignment statement provides a convenient and succinct notation for specifying data-parallel operations. However, it applies only to a limited set of such operations. For example, it requires that operands of right-hand-side expressions be conformant with (of the same shape as) the left-hand-side array. Two other HPF constructs allow an explicitly parallel representation of a wider range of data-parallel operations. These are the FORALL statement and the INDEPENDENT directive.
The FORALL statement allows for more general assignments to sections of an array. A FORALL statement has the general form
FORALL ( triplet, ..., triplet, mask ) assignmentwhere assignment is an arithmetic or pointer assignment and triplet has the general form
subscript = lower-bound : upper-bound : stride(with : stride being optional) and specifies a set of indices.
The assignment statement is evaluated for those index values specified by the list of triplets that are not rejected by the optional mask. For example, the following statements set each element of X to the sum of its indices, zero the upper right triangle of Y, and zero the diagonal of Z, respectively.
FORALL (i=1:m, j=1:n) X(i,j) = i+j
FORALL (i=1:n, j=1:n, i<j) Y(i,j) = 0.0
FORALL (i=1:n) Z(i,i) = 0.0
A FORALL statement is evaluated as follows. First, the right-hand-side expression is evaluated for all index values; these evaluations can be performed in any order. Second, the assignments are performed, again in any order. To ensure determinism, a FORALL statement cannot assign to the same element of an array more than once. A compiler can attempt to detect that this requirement is violated but is not required to do so. Hence, the following statement is valid only if the array Index does not contain duplicate values.
FORALL (i=1:n) A(Index(i)) = B(i)
 .
. Use of FORALL:
Use of FORALL:
The array assignment used to update the array New in Program 7.2 can also be expressed using FORALL, as follows.
forall(i=2:99, j=2:99)$ New(i,j) = (X(i-1, j) + X(i+1, j) +
$ X(i, j-1) + X(i, j+1))/4
Of course, in this case there is no reason not to use an array assignment.
An HPF program can reveal additional opportunities for parallel execution by using the INDEPENDENT directive to assert that the iterations of a do-loop can be performed independently---that is, in any order or concurrently---without changing the result computed. In effect, this directive changes a do-loop from an implicitly parallel construct to an explicitly parallel construct.
The INDEPENDENT directive must immediately precede the do-loop to which it applies. In its simplest form, it has no additional argument and asserts simply that no iteration of the do-loop can affect any other iteration. (An iteration I affects an iteration J if I leads to an assignment to a value read by J .) For example, in the following code fragment the assertion implies both that the array Index does not contain duplicate indices and that A and B do not share storage, for example because of an equivalence statement.
!HPF$ INDEPENDENT
do i=1,n
A(Index(i)) = B(i)
enddo
In the following code fragment, the directives indicate that the outer two loops are independent. The inner loop assigns elements of A repeatedly and hence is not independent.
!HPF$ INDEPENDENTdo i=1,n1 ! Loop over i independent
!HPF$ INDEPENDENT
do j=1,n2 ! Loop over j independent
do k=1,n3 ! Inner loop not independent
A(i,j) = A(i,j) + B(i,j,k)*C(i,j)
enddo
enddo
enddo
An INDEPENDENT directive can also specify that the assertion would be correct if distinct storage were to be used for a specified set of variables for each iteration of the nested do-loop. This is achieved by postfixing a NEW specifier, as in the following example. In this code fragment, interleaved execution of different loop iterations would cause erroneous results if values of tmp1 and tmp2 computed in one iteration were used in another. The NEW specifier ensures that this situation does not arise.
!HPF$ INDEPENDENT
do i=1,n1
!HPF$ INDEPENDENT, NEW(tmp1,tmp2)
do j=1,n2
tmp1 = B(i,j) + C(i,j)
tmp1 = B(i,j) - C(i,j)
A(i,j) = tmp1*tmp2
ENDDO
ENDDO
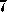 .
. Parallel Fast Fourier Transform:
Parallel Fast Fourier Transform:
A 2-D FFT applies a 1-D FFT operation first to each column of a two-dimensional array and then to each row. An initial column distribution allows the first set of FFTs to proceed without communication; the array is then transposed before performing the second set of FFTs. (A similar technique is used in Section 4.4, but here we distribute by column to improve locality in a Fortran implementation.) The transpose involves considerable communication but is frequently more efficient than an algorithm based on a static decomposition and parallel FFTs. Program 7.4 implements the transpose algorithm. Notice the initial distribution of A (blocked, by column) and the call to the transpose intrinsic. Notice also the use of the INDEPENDENT directive to specify that the colfft calls in the do-loop can proceed independently, even though each is passed the entire A array. This assertion is valid because each call to colfft operates on a single column.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
© Copyright 1995 by Ian Foster