The convolution theorem for z transforms states that for any (real or
complex) signals ![]() and
and ![]() ,
convolution in the time domain is multiplication in the
,
convolution in the time domain is multiplication in the
![]() domain, i.e.,
domain, i.e.,
Proof:
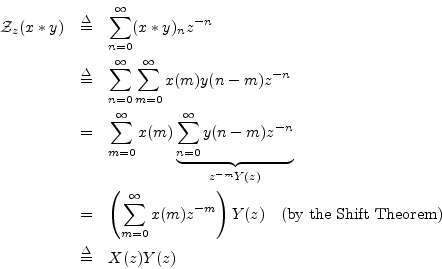
The convolution theorem provides a major cornerstone of linear systems theory. It implies, for example, that any LTI filter (recursive or nonrecursive) can be implemented by convolving the input signal with the impulse response of the filter, as shown in the next section.