When ![]() in Eq. (6.7), we may perform a step of long division
of
in Eq. (6.7), we may perform a step of long division
of ![]() to produce an FIR part in parallel with a
strictly proper IIR part, e.g.,
to produce an FIR part in parallel with a
strictly proper IIR part, e.g.,
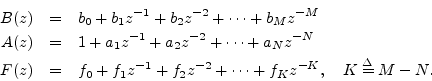
When ![]() , we define
, we define ![]() . This type of decomposition is
computed by the residuez function in the Matlab Signal
Processing Tool Box (a function for computing a complete partial
fraction expansion, as illustrated in §6.8.8 below). In
Octave, which doesn't have
residuez as of this writing, the same result can be obtained
using its residue function, as derived in §H.5.
. This type of decomposition is
computed by the residuez function in the Matlab Signal
Processing Tool Box (a function for computing a complete partial
fraction expansion, as illustrated in §6.8.8 below). In
Octave, which doesn't have
residuez as of this writing, the same result can be obtained
using its residue function, as derived in §H.5.
An alternate FIR part is obtained by performing long division on the reversed polynomial coefficients to obtain
We may compare these two PFE alternatives as follows.
Let ![]() denote
denote ![]() ,
,
![]() , and
, and
![]() .
(I.e., we use a subscript to indicate polynomial order, and `
.
(I.e., we use a subscript to indicate polynomial order, and `![]() ' is
omitted for notational simplicity.) Then for
' is
omitted for notational simplicity.) Then for
![]() we have two cases:
we have two cases:
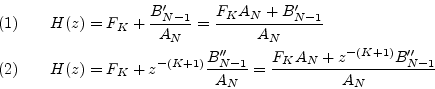
In the first form, the
![]() coefficients are ``left
justified'' in the reconstructed numerator, while in the second form
they are ``right justified''. The second form is generally more
efficient for modeling purposes, since the numerator of the IIR
part (
coefficients are ``left
justified'' in the reconstructed numerator, while in the second form
they are ``right justified''. The second form is generally more
efficient for modeling purposes, since the numerator of the IIR
part (
![]() ) can be used to match additional
terms in the impulse response after the FIR part
) can be used to match additional
terms in the impulse response after the FIR part ![]() has
``died out''.
has
``died out''.
In summary, an arbitrary digital filter transfer function ![]() with
with
![]() distinct poles can always be expressed as a parallel combination
of complex one-pole filters, together with a parallel FIR part
when
distinct poles can always be expressed as a parallel combination
of complex one-pole filters, together with a parallel FIR part
when ![]() . When there is an FIR part, the strictly proper IIR
part may be delayed such that its impulse response begins where that
of the FIR part leaves off.
. When there is an FIR part, the strictly proper IIR
part may be delayed such that its impulse response begins where that
of the FIR part leaves off.
In artificial reverberation applications, the FIR part may correspond to the early reflections, while the IIR part provides the late reverb, which is typically dense, smooth, and exponentially decaying [86]. The predelay (``pre-delay'') control in some commercial reverberators is the amount of pure delay at the beginning of the reverberator's impulse response. Thus, neglecting the early reflections, the order of the FIR part can be viewed as the amount of predelay for the IIR part.