A signal which has no negative-frequency components is called an
analytic signal.4.12 Therefore, in continuous time, every analytic signal
![]() can be represented as
can be represented as
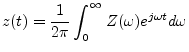
Any real sinusoid
![]() may be converted to a
positive-frequency complex sinusoid
may be converted to a
positive-frequency complex sinusoid
![]() by simply generating a phase-quadrature component
by simply generating a phase-quadrature component
![]() to serve as the ``imaginary part'':
to serve as the ``imaginary part'':
For more complicated signals which are expressible as a sum of many
sinusoids, a filter can be constructed which shifts each
sinusoidal component by a quarter cycle. This is called a
Hilbert transform filter. Let
![]() denote the output
at time
denote the output
at time ![]() of the Hilbert-transform filter applied to the signal
of the Hilbert-transform filter applied to the signal ![]() .
Ideally, this filter has magnitude
.
Ideally, this filter has magnitude ![]() at all frequencies and
introduces a phase shift of
at all frequencies and
introduces a phase shift of ![]() at each positive frequency and
at each positive frequency and
![]() at each negative frequency. When a real signal
at each negative frequency. When a real signal ![]() and
its Hilbert transform
and
its Hilbert transform
![]() are used to form a new complex signal
are used to form a new complex signal
![]() ,
the signal
,
the signal ![]() is the (complex) analytic signal corresponding to
the real signal
is the (complex) analytic signal corresponding to
the real signal ![]() . In other words, for any real signal
. In other words, for any real signal ![]() , the
corresponding analytic signal
, the
corresponding analytic signal
![]() has the property
that all ``negative frequencies'' of
has the property
that all ``negative frequencies'' of ![]() have been ``filtered out.''
have been ``filtered out.''
To see how this works, recall that these phase shifts can be impressed on a
complex sinusoid by multiplying it by
![]() . Consider
the positive and negative frequency components at the particular frequency
. Consider
the positive and negative frequency components at the particular frequency
![]() :
:
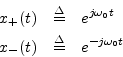
Now let's apply a ![]() degrees phase shift to the positive-frequency
component, and a
degrees phase shift to the positive-frequency
component, and a ![]() degrees phase shift to the negative-frequency
component:
degrees phase shift to the negative-frequency
component:
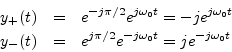
Adding them together gives
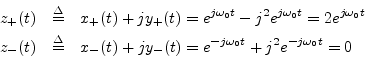
and sure enough, the negative frequency component is filtered out. (There is also a gain of 2 at positive frequencies which we can remove by defining the Hilbert transform filter to have magnitude 1/2 at all frequencies.)
For a concrete example, let's start with the real sinusoid
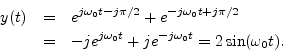
The analytic signal is then
![\includegraphics[width=2.8in]{eps/sineFD}](img572.png) |
Figure 4.16 illustrates what is going on in the frequency domain.
At the top is a graph of the spectrum of the sinusoid
![]() consisting of impulses at frequencies
consisting of impulses at frequencies
![]() and
zero at all other frequencies (since
and
zero at all other frequencies (since
![]() ). Each impulse
amplitude is equal to
). Each impulse
amplitude is equal to ![]() . (The amplitude of an impulse is its
algebraic area.) Similarly, since
. (The amplitude of an impulse is its
algebraic area.) Similarly, since
![]() , the spectrum of
, the spectrum of
![]() is an impulse of amplitude
is an impulse of amplitude ![]() at
at
![]() and amplitude
and amplitude ![]() at
at
![]() .
Multiplying
.
Multiplying ![]() by
by ![]() results in
results in
![]() which is shown in
the third plot, Fig.4.16c. Finally, adding together the first and
third plots, corresponding to
which is shown in
the third plot, Fig.4.16c. Finally, adding together the first and
third plots, corresponding to
![]() , we see that the
two positive-frequency impulses add in phase to give a unit
impulse (corresponding to
, we see that the
two positive-frequency impulses add in phase to give a unit
impulse (corresponding to
![]() ), and at frequency
), and at frequency
![]() , the two impulses, having opposite sign,
cancel in the sum, thus creating an analytic signal
, the two impulses, having opposite sign,
cancel in the sum, thus creating an analytic signal ![]() ,
as shown in Fig.4.16d. This sequence of operations illustrates
how the negative-frequency component
,
as shown in Fig.4.16d. This sequence of operations illustrates
how the negative-frequency component
![]() gets
filtered out by summing
gets
filtered out by summing
![]() with
with
![]() to produce the analytic signal
to produce the analytic signal
![]() corresponding
to the real signal
corresponding
to the real signal
![]() .
.
As a final example (and application), let
![]() ,
where
,
where ![]() is a slowly varying amplitude envelope (slow compared
with
is a slowly varying amplitude envelope (slow compared
with ![]() ). This is an example of amplitude modulation
applied to a sinusoid at ``carrier frequency''
). This is an example of amplitude modulation
applied to a sinusoid at ``carrier frequency'' ![]() (which is
where you tune your AM radio). The Hilbert transform is very close to
(which is
where you tune your AM radio). The Hilbert transform is very close to
![]() (if
(if ![]() were constant, this would
be exact), and the analytic signal is
were constant, this would
be exact), and the analytic signal is
![]() .
Note that AM demodulation4.14is now nothing more than the absolute value. I.e.,
.
Note that AM demodulation4.14is now nothing more than the absolute value. I.e.,
![]() . Due to this simplicity, Hilbert transforms are sometimes
used in making
amplitude envelope followers for narrowband signals (i.e., signals with all energy centered about a single ``carrier'' frequency).
AM demodulation is one application of a narrowband envelope follower.
. Due to this simplicity, Hilbert transforms are sometimes
used in making
amplitude envelope followers for narrowband signals (i.e., signals with all energy centered about a single ``carrier'' frequency).
AM demodulation is one application of a narrowband envelope follower.