In the signal processing literature, it is common to write the DFT
and its inverse in the
more pure form below, obtained by setting ![]() in the previous definition:
in the previous definition:
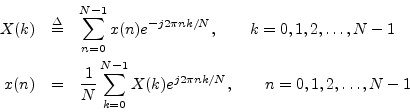
where ![]() denotes the input signal at time (sample)
denotes the input signal at time (sample) ![]() , and
, and ![]() denotes the
denotes the ![]() th spectral sample. This form is the simplest
mathematically, while the previous form is easier to interpret
physically.
th spectral sample. This form is the simplest
mathematically, while the previous form is easier to interpret
physically.
There are two remaining symbols in the DFT we have not yet defined:
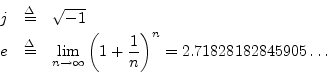
The first,
![]() , is the basis for complex
numbers.1.1 As a result, complex numbers will be the
first topic we cover in this book (but only to the extent needed
to understand the DFT).
, is the basis for complex
numbers.1.1 As a result, complex numbers will be the
first topic we cover in this book (but only to the extent needed
to understand the DFT).
The second,
![]() , is a (transcendental) real number
defined by the above limit. We will derive
, is a (transcendental) real number
defined by the above limit. We will derive ![]() and talk about why it
comes up in Chapter 3.
and talk about why it
comes up in Chapter 3.
Note that not only do we have complex numbers to contend with, but we have them appearing in exponents, as in
With ![]() ,
, ![]() , and imaginary exponents understood, we can go on to prove
Euler's Identity:
, and imaginary exponents understood, we can go on to prove
Euler's Identity:
Finally, we need to understand what the summation over ![]() is doing in
the definition of the DFT. We'll learn that it should be seen as the
computation of the inner product of the signals
is doing in
the definition of the DFT. We'll learn that it should be seen as the
computation of the inner product of the signals ![]() and
and ![]() defined above, so that we may write the DFT, using inner-product
notation, as
defined above, so that we may write the DFT, using inner-product
notation, as
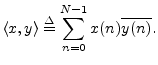
After the foregoing, the inverse DFT can be understood as the
sum of projections of ![]() onto
onto
![]() ; i.e.,
we'll show
; i.e.,
we'll show
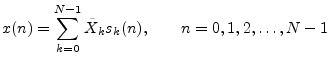
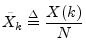
Having completely understood the DFT and its inverse mathematically, we go on to proving various Fourier Theorems, such as the ``shift theorem,'' the ``convolution theorem,'' and ``Parseval's theorem.'' The Fourier theorems provide a basic thinking vocabulary for working with signals in the time and frequency domains. They can be used to answer questions such as
``What happens in the frequency domain if I do [operation x] in the time domain?''Usually a frequency-domain understanding comes closest to a perceptual understanding of audio processing.
Finally, we will study a variety of practical spectrum analysis examples, using primarily the matlab programming language [65] to analyze and display signals and their spectra.