AVL Search Trees

The problem with binary search trees is that while the average running times for search, insertion, and withdrawal operations are all , any one operation is still O(n) in the worst case. This is so because we cannot say anything in general about the shape of the tree.

For example, consider the two binary search trees shown Figure . Both trees contain the same set of keys. The tree is obtained by starting with an empty tree and inserting the keys in the following order

The tree is obtained by starting with an empty tree and inserting the keys in this order

Clearly, is a better tree search tree than . In fact, since is a perfect binary tree , its height is . Therefore, all three operations, search, insertion, and withdrawal, have the same worst case asymptotic running time, .

The reason that is better than is that it is the more balanced tree. If we could ensure that the search trees we construct are balanced then the worst-case running time of search, insertion, and withdrawal, could be made logarithmic rather than linear. But under what conditions is a tree balanced?

If we say that a binary tree is balanced if the left and right subtrees of every node have the same height, then the only trees which are balanced are the perfect binary trees. A perfect binary tree of height h has exactly internal nodes. Therefore, it is only possible to create perfect trees with n nodes for . Clearly, this is an unsuitable balance condition because it is not possible to create a balanced tree for every n.

What are the characteristics of a good balance condition ?

1. A good balance condition ensures that the height of a tree with n nodes is .
2. A good balance condition can be maintained efficiently. I.e., the additional work necessary to balance the tree when an item is inserted or deleted is O(1).

Definition (AVL Balance Condition)  An empty binary tree is AVL balanced  . A non-empty binary tree, , is AVL balanced if both and are AVL balanced and

where is the height of and is the height of .

Clearly, all perfect binary trees are AVL balanced. What is not so clear is that heights of all trees that satisfy the AVL balance condition are logarithmic in the number of internal nodes.

Theorem  The height, h, of an AVL balanced tree with n internal nodes satisfies

extbfProof The lower bound follows directly from Theorem . It is in fact true for all binary trees regardless of whether they are AVL balanced.

To determine the upper bound, we turn the problem around and ask the question, what is the minimum number of internal nodes in an AVL balanced tree of height h?

Let represent an AVL balanced tree of height h which has the smallest possible number of internal nodes, say . Clearly, must have at least one subtree of height h-1 and that subtree must be . To remain AVL balanced, the other subtree can have height h-1 or h-2. Since we want the smallest number of internal nodes, it must be . Therefore, the number of internal nodes in is , where .

Clearly, contains a single internal node, so . Similarly, contains exactly two nodes, so . Thus, is given by the recurrence

The remarkable thing about Equation  is its similarity with the definition of Fibonacci numbers  (Equation ). In fact, it can easily be shown by induction that

for all , where is the Fibonacci number.

Base Cases

Inductive Hypothesis Assume that for . Then

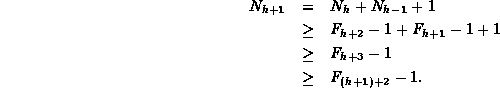
Therefore, by induction on k, , for all .

According to Theorem , the Fibonacci numbers are given by

where and . Furthermore, since , .

Therefore,

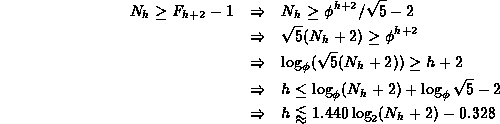
This completes the proof of the upper bound.

So, we have shown that the AVL balance condition satisfies the first criterion of a good balance condition--the height of an AVL balanced tree with n internal nodes is . What remains to be shown is that the balance condition can be efficiently maintained. To see that it can, we need to look at an implementation.

• Implementing AVL Trees
• Inserting Items into an AVL Tree
• Removing Items from an AVL Tree

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.