Exercises

1.   For each of the following key sequences determine the binary search tree obtained when the keys are inserted one-by-one in the order given into an initially empty tree:
   1. 1, 2, 3, 4, 5, 6, 7.
   2. 4, 2, 1, 3, 6, 5, 7.
   3. 1, 6, 7, 2, 4, 3, 5.
2.   For each of the binary search trees obtained in Exercise  determine the tree obtained when the root is withdrawn.
3. Repeat Exercises  and  for AVL trees.
4. Derive an expression for the total space needed to represent a tree of n internal nodes using each of the following classes:
   1. BST defined in Program ,
   2. AVLTree defined in Program ,
   3. MWayTree defined in Program , and
   4. BTree defined in Program .
   Hint: For the MWayTree and BTree assume that the tree contains are k keys, where .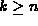
5. To delete a non-leaf node from a binary search tree, we swap it either with the smallest key its right subtree or with the largest key in its left subtree and then recursively delete it from the subtree. In a tree of n nodes, what its the maximum number of swaps needed to delete a key?
6. Devise an algorithm to compute the internal path length of a tree. What is the running time of your algorithm?
7. Devise an algorithm to compute the external path length of a tree. What is the running time of your algorithm?
8. Suppose that you are given a sorted sequence of n keys, 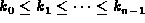, to be inserted into a binary search tree.
   1. What is the minimum height of a binary tree that contains n nodes.
   2. Devise an algorithm to insert the given keys into a binary search tree so that the height of the resulting tree is minimized.
   3. What is the running time of your algorithm?
9. Devise an algorithm to construct an AVL tree of a given height h that contains the minimum number of nodes. The tree should contain the keys 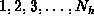, where 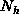is given by Equation .
10. Consider what happens when we insert the keys 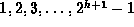one-by-one in the order given into an initially empty AVL tree for 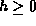. Prove that the result is always a perfect tree of height h.
11.   The Find routine defined in Program  is recursive. Write a non-recursive routine to find a given item in a binary search tree.
12. Repeat Exercise  for the FindMin function defined in Program .
13. Devise an algorithm to select the 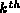key in a binary search tree. E.g., given a tree with n nodes, k=0 selects the smallest key, k=n-1 selects the largest key, and 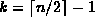selects the median key.
14. Devise an algorithm to test whether a given binary search tree is AVL balanced. What is the running time of your algorithm?
15. Devise an algorithm that takes two values, a and b such tha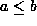t , and which visits all the keys x in a binary search tree such that 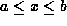. The running time of your algorithm should be 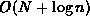, where N is the number of keys visited and n is the number of keys in the tree.
16. Devise an algorithm to merge the contents of two binary search trees into one. What is the running time of your algorithm?
17.   (This question should be attempted after reading Chapter ). Prove that a complete binary tree (Definition ) is AVL balanced.
18. Do Exercise .
19.   For each of the following key sequences determine the 3-way search tree obtained when the keys are inserted one-by-one in the order given into an initially empty tree:
    1. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
    2. 3, 1, 4, 5, 9, 2, 6, 8, 7, 0.
    3. 2, 7, 1, 8, 4, 5, 9, 0, 3, 6.
20. Repeat Exercise  for B-trees of order 3.

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.