Connectedness of an Undirected Graph

Data Structures and Algorithms with Object-Oriented Design Patterns in C++

Connectedness of an Undirected Graph

Definition (Connectedness of an Undirected Graph) An undirected graph is connected if there is a path in G between every pair of vertices in .

Consider the undirected graph shown in Figure . It is tempting to interpret this figure as a picture of two graphs. However, the figure actually represents the undirected graph , given by

Clearly, the graph is not connected. For example, there is no path between vertices a and d. In fact, the graph consists of two, unconnected parts, each of which is a connected sub-graph. The connected sub-graphs of a graph are called connected components .

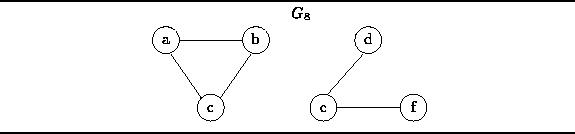
Figure: An Unconnected, Undirected Graph with Two (Connected) Components

A traversal of an undirected graph (either depth-first or breadth-first) starting from any vertex will only visit all the other vertices of the graph if that graph is connected. Therefore, there is a very simply way to test whether an undirected graph is connected: Count the number of vertices visited during a traversal of the graph. Only if all the vertices are visited is the graph connected.

Program shows how this can be implemented. The IsConnected member function of the Graph class is a Boolean-valued accessor that returns true if the graph is connected. The routine is implemented using a CountingVisitor and the DepthFirstTraversal routine.

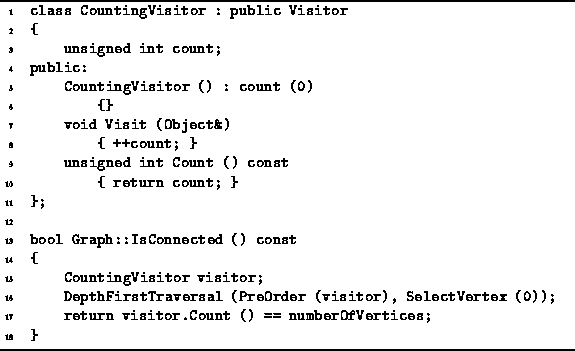
program51016
Program: Graph Class IsConnected Member Function Definition

A CountingVisitor is a visitor that simply counts the number of vertices it visits. It has a single member variable, count, which is initialized to zero in the constructor. The Visit routine adds one the count each time it is called and the Count accessor returns the value of the count.

The worst-case running time of the IsConnected routine is determined by the time taken by the DepthFirstTraversal. Clearly in this case . Therefore, the running time of IsConnected is when adjacency matrices are used to represent the graph and when adjacency lists are used.