Connectedness of a Directed Graph

When dealing with directed graphs, we define two kinds of connectedness, strong and weak. Strong connectedness of a directed graph is defined as follows:

Definition (Strong Connectedness of a Directed Graph)   A directed graph is strongly connected   if there is a path in G between every pair of vertices in .

For example, Figure  shows the directed graph given by

Notice that the graph is not connected! E.g., there is no path from any of the vertices in to any of the vertices in . Nevertheless, the graph ``looks'' connected in the sense that it is not made of up of separate parts in the way that the graph in Figure  is.

This idea of ``looking'' connected is what weak connectedness represents. To define weak connectedness we need to introduce first the notion of the undirected graph that underlies a directed graph: Consider a directed graph . The underlying undirected graph is the graph where represents the set of undirected edges that is obtained by removing the arrowheads from the directed edges in G:

  
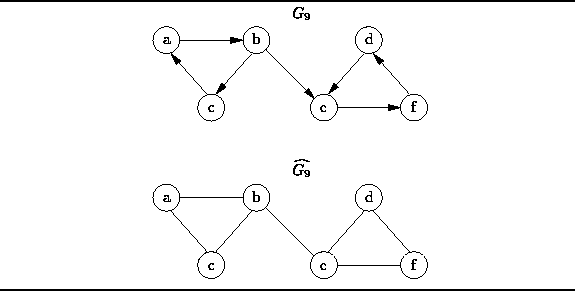
Figure: An Weakly Connected Directed Graph and the Underlying Undirected Graph

Weak connectedness of a directed graph is defined with respect to its underlying, undirected graph:

Definition (Weak Connectedness of a Directed Graph) A directed graph is weakly connected   if the underlying undirected graph is connected.

For example, since the undirected graph in Figure  is connected, the directed graph is weakly connected. Consider what happens when we remove the edge (b,e) from the directed graph . The underlying undirected graph that we get is in Figure . Therefore, when we remove edge (b,e) from , the graph that remains is neither strongly connected nor weakly connected.

A traversal of a directed graph (either depth-first or breadth-first) starting from a given vertex will only visit all the vertices of an undirected graph if there is a path from the start vertex to every other vertex. Therefore, a simple way to test whether a directed graph is strongly connected uses traversals--one starting from each vertex in . Each time the number of vertices visited is counted. The graph is strongly connected if all the vertices are visited in each traversal.

Program  shows how this can be implemented. It shows the IsConnected member function of the Digraph class which returns the Boolean value true if the graph is strongly connected.

  
Program: Digraph Class IsConnected Member Function Definition

The routine consists of a loop over all the vertices of the graph. Each iteration does a DepthFirstTraversal using the CountingVisitor given in Program . The running time for one iteration is essentially that of the DepthOrderTraversal since for the counting visitor. Therefore, the worst-case running time for the IsConnected routine is when adjacency matrices are used and when adjacency lists are used to represent the graph.

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.