About Polynomials Again

In this section we reexamine the asymptotic behavior of polynomials in n. In Section  we showed that . That is, f(n) grows asymptotically no more quickly than . This time we are interested in the asymptotic lower bound rather than the asymptotic upper bound. We will see that as n gets large, the term involving also dominates the lower bound in the sense that f(n) grows asymptotically as quickly as . I.e., that .

Theorem  Consider a polynomial  in n of the form

where . Then .

extbfProof We begin by taking the term out of the summation:

Since, n is a non-negative integer and , the term is positive. For each of the remaining terms in the summation, . Hence

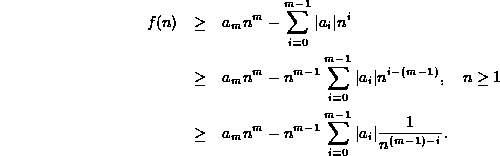
Note that for integers , for . Thus

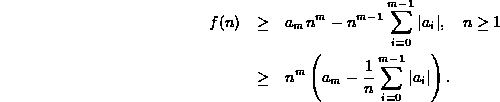
Consider the term in parentheses on the right. What we need to do is to find a positive constant c and an integer so that for all integers this term is greater than or equal to c:

We choose the value for which the term is greater than zero:

The value will suffice! Thus

From Equation  we see that we have found the constants and c, such that for all , . Thus, .

This property of the asymptotic behavior of polynomials is used extensively. In fact, whenever we have a function, which is a polynomial in n, we will immediately ``drop'' the less significant terms (i.e., terms involving powers of n which are less than m), as well as the leading coefficient, , to write .

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.